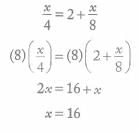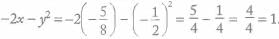GMAT Classic Mock Test - 2 - GMAT MCQ
30 Questions MCQ Test - GMAT Classic Mock Test - 2
Working at a constant rate, a copy machine makes 20 copies of a one-page document per minute. If the machine works at this constant rate, how many hours does it take to make 4,800 copies of a one-page document?
The sum S of the first n consecutive positive even integers is given by S = n(n +1). For what value of n is this sum equal to 110?
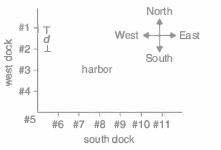
A certain harbor has docking stations along its west and south docks, as shown in the figure; any two adjacent docking stations are separated by a uniform distance d. A certain boat left the west dock from docking station #2 and moved in a straight line diagonally until it reached the south dock. If the boat was at one time directly east of docking station #4 and directly north of docking station #7, at which docking station on the south dock did the boat arrive?
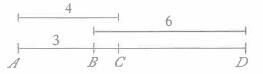
Points A, B, C, and D, in that order, lie on a line. If AB = 3 cm, AC = 4 cm, and BD = 6 cm, what is CD, in
centimeters?
What is the value of x2yz - xyz2, if x = -2, y = 1, and z = 3?
A company sells radios for $15.00 each. It costs the company $14.00 per radio to produce 1,000 radios and $13.50 per radio to produce 2,000 radios. How much greater will the company's gross profit be from the production and sale of 2,000 radios than from the production and sale of 1,000 radios?
Which of the following represent positive numbers?
I. -3 - (-5)
II. (-3)(-5)
Ill. -5 - (-3)
Point X lies on side BC of rectangle ABCD, which has length 12 and width 8. What is the area of triangular region AXD?
A grocer has 400 pounds of coffee in stock, 20 percent of which is decaffeinated. If the grocer buys another 100 pounds of coffee of which 60 percent is decaffeinated, what percent, by weight, of the grocer's stock of coffee is decaffeinated?
The toll T, in dollars, for a truck using a certain bridge is given by the formula T = 1.50 + 0.50(x - 2), where x is the number of axles on the truck. What is the toll for an 18-wheel truck that has 2 wheels on its front axle and 4 wheels on each of its other axles?
For what value of x between -4 and 4, inclusive, is the value of x2 - 10x + 16 the greatest?
If x = -5/8 and y = -1/2, what is the value of the expression -2x - y2 ?
What is the value of x3 + y3?
1. x + y = 12
2. x -y = 8
What is the area of triangle ABC?
1. ∠ ABC and ∠CAB have the same measure.
2. AB = 9, BC = 12, and CA = 15.
The mean (average) of w, x, and y is z.Is z = w?
1. 1/2(x + y) = w
2. w = x = y
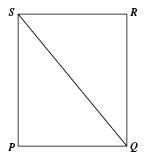
What is the area of square PQRS?
1. The perimeter of PQRS is 28.
2. The diagonal SQ is 7√2.
A piece of wood is cut into three pieces that have lengths in the ratio x : y : z = 1:2:3. What is the length x + y + z?
1. x + z = 16
2. x < y < z
How is Bill related to Betty?
(1) Cindy, the wife of Bill's only brother Chris does not have any siblings.
(2) Betty is Cindy's brother in law's wife.
Is y an integer?
(1) y3 is an integer
(2) 3y is an integer
If a salesman received a commission of 3% of the sales that he has booked in a month, what was the sales booked by the salesman in the month of November 2003?
(1) The sales booked by the salesman in the month of November 2003 minus salesman's commission was $245,000
(2) The selling price of the sales booked by the salesman in the month of November 2003 was 125 percent of the original purchase price of $225,000
Is the positive integer 'x' divisible by 12?
(1) x is divisible by 6
(2) x is divisible by 8
When the positive integer Y is divided by 2, is the remainder 1?
(A) (-1)(Y + 2) = -1
(B) Y is prime
Is the two digit positive integer P a prime number?
(1) (P + 2) and (P - 2) are prime.
(2) (P - 4) and (P + 4) are prime.
If m, s are the average and standard deviation of integers a, b, c, and d, is s > 0?
(1) m > a
(2) a + b + c + d = 0