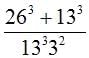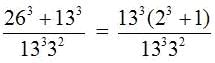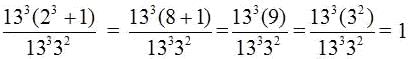All Courses
Get the App Signup / Login
Sign in Open App
GMAT Exam  >  GMAT Tests  >  GMAT Classic Mock Test - 6 - GMAT MCQ

GMAT Classic Mock Test - 6 - GMAT MCQ


Test Description

30 Questions MCQ Test - GMAT Classic Mock Test - 6

GMAT Classic Mock Test - 6 for GMAT 2024 is part of GMAT preparation. The GMAT Classic Mock Test - 6 questions and answers have been prepared according to the GMAT exam syllabus.The GMAT Classic Mock Test - 6 MCQs are made for GMAT 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for GMAT Classic Mock Test - 6 below.
Solutions of GMAT Classic Mock Test - 6 questions in English are available as part of our course for GMAT & GMAT Classic Mock Test - 6 solutions in Hindi for GMAT course. Download more important topics, notes, lectures and mock test series for GMAT Exam by signing up for free. Attempt GMAT Classic Mock Test - 6 | 76 questions in 158 minutes | Mock test for GMAT preparation | Free important questions MCQ to study for GMAT Exam | Download free PDF with solutions
GMAT Classic Mock Test - 6 - Question 1
Save

A test maker is to design a probability test from a list of 21 questions. The 21 questions are classified into three categories: hard, intermediate and easy. If there are 7 questions in each category and the test maker is to select two questions from each category, how many different combinations of questions can the test maker put on the test?

Detailed Solution for GMAT Classic Mock Test - 6 - Question 1
  1. In this problem order is not important. For example, the selection of question 1, 8 and 21 is the same as the selection of question 21, 8 and 1. Since order is unimportant, the combination formula applies.
  2. The formula for a combination is:
    nCr= n!/((n - r)!r!)
    where n is the total number of selections available and r is the number of items to be selected.
  3. Since the test maker must select a total of six questions and two questions from each category, the combination formula is used. Since there are 3 categories and two questions will be selected for each of the 3 categories, total number of combinations is:
    =7C2 x 7C2 x 7C2
  4. There are a total of (7C2)3 combinations.
GMAT Classic Mock Test - 6 - Question 2
Save

If the sum of the consecutive integers from –35 to n inclusive is 150, what is the value of n?A

Detailed Solution for GMAT Classic Mock Test - 6 - Question 2
  1. Consecutive integers are integers that follow in sequence, where the difference between two successive integers is 1. You are told that the sum of the consecutive integers from –35 to n inclusive is 150. The sum of all the consecutive numbers from –35 to –1 will be negative, yet the sum of the entire set is positive. This means that there must be positive integers in the set that go beyond +35 to result in a positive sum.
  2. Consider that a number plus its opposite sum to zero:
    –5 + 5 = 0, –13 + 13 = 0, etc.
    Therefore:
    (–35) + (–34) + … + (–1) + 0 + 1 + … + 34 + 35 = 0
  3. The next consecutive number in the set would be 36. Could this be n? If it were the sum of the set would be 0 + 36 = 36. So there must be more integers in the set. Move forward one number at a time, until the sum is 150:
    0 + 36 = 36
    36 + 37 = 73
    73 + 38 = 111
    111 + 39 = 150
  4. Since the addition of 39 makes the sum 150, it must be the last consecutive integer in the set and the value of n. Therefore choice (B) is correct.
1 Crore+ students have signed up on EduRev. Have you? Download the App
GMAT Classic Mock Test - 6 - Question 3
Save

A box contains either blue or red flags. The total number of flags in the box is an even number. A group of children are asked to pick up two flags each. If all the flags are used up in the process such that 60% of the children have blue flags, and 55% have red flags, what percentage of children have flags of both the colors?

Detailed Solution for GMAT Classic Mock Test - 6 - Question 3
  1. In this problem, let A be the event that a child picks up a blue flag, B be the event that a child picks up a red flag. Then, A∪B is the event that the child picks up either a blue or a red flag, and A∩B is the event that the child picks up both a blue and a red flag.
  2. From the problem statement we know:
    I. P(AUB) = 100% (Since there are even number of flags and all the flags in the box are taken by the children)
    II. P(A) = 60%
    III.P(B) = 55%
    IV. P(A∩B)=?
  3. We are trying to find the percentage of children who have flags of both the colors. Substituting the values from (3.) into the equation given in (1.) we get:
  4. P(A∪B) = P(A) + P(B) - P(A∩B)
    100% = 60% + 55% - P(A∩B)
    P(A∩B) = (60% +55%)-100%
    P(A∩B) =115%-100%
    P(A∩B) =15%
    Therefore the percentage of children who got both a red flag and a blue flag is 15%. Thus, C is the correct answer choice.
GMAT Classic Mock Test - 6 - Question 4
Save

A coin has two sides. One side has the number 1 on it and the other side has the number 2 on it. If the coin is flipped three times what is the probability that the sum of the numbers on the landing side of the coin will be greater than 4?
Detailed Solution for GMAT Classic Mock Test - 6 - Question 4
  1. One approach to solve the problem is to list the different possibilities for a toss of coin three times. Because there are two outcomes and the coin is tossed three times, the table will have 2 x 2 x 2 or 8 rows.
  2. Next add the resulting rows together to find the sum (the fourth column in the table below).
  3. From the table we see that there are 4 situations where the sum of the tosses will be greater than 4. And there are 8 possible combinations resulting in a probability of
  4. 4/8 or a probability of 1/2. SO the correct answer is D.
GMAT Classic Mock Test - 6 - Question 5
Save

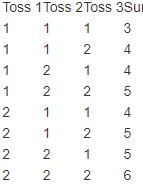
There are five empty chairs in a row. If six men and four women are waiting to be seated, what is the probability that the seats will be occupied by two men and three women?
Detailed Solution for GMAT Classic Mock Test - 6 - Question 5
  1. This is a combination-probability problem. To solve this we will need to find out the number of ways we can choose 2 men out of 6 and 3 women out of 4 to sit in the chair.
  2. Next, we note that the probability of seating two men and three women in the empty chairs is:
    (number of ways of choosing 2 men and 3 women)/ (number of ways of seating five people out of ten).
  3. The total number of ways of choosing five people to sit out of a total of ten (six men + four women) is given by:
    10C5 = 10!/([10-5]!5!)
    = (10 x 9 x 8 x 7 x 6)/[10-5]!
    = (10 x 9 x 8 x 7 x 6)/5!
    = 252
  4. Now we want the seats to be taken by 2 men and 3 women.
    I. The number of ways to choose 2 men out of six to occupy the seat is given by:
    6C2 = 6!/4! x 2! = 15
    II. The number of ways to choose 3 women out of 4 to sit is given by:
    4C3 = 4!/3! x 1! = 4
  5. Using the multiplication principle, the total number of ways to select two men and three women is:
    15 x 4=60
  6. The probability is thus = 60/252
    = (12 x 5)/(12 x 21)
    = 5/21. Hence the correct answer choice is B
GMAT Classic Mock Test - 6 - Question 6
Save

In baseball, the batting average is defined as the ratio of a player’s hits to at bats. If a player had anywhere from 4 to 6 at bats in a recent game and had anywhere from 2 to 3 hits in the same game, the player’s actual batting average for that game could fall anywhere between
Detailed Solution for GMAT Classic Mock Test - 6 - Question 6
  1. The ratio of a batting average is a fraction. As you decrease the numerator or increase the denominator, the fraction becomes smaller. Likewise, as you increase the numerator or decrease the denominator, the fraction becomes larger.
  2. In the case of a batting average, the numerator is "hits" (H) while the denominator is "at bats" (B). Thus, the ratio we are looking at is:
    H/B, where 2 < H <3 and 4 < B <6.
  3. To find the lowest value that the batting average could be, we want to assume the lowest numerator (hits of 2) and the highest denominator (at bats of 6): 2/6 = 0.333.
  4. Likewise, to find the highest value that the batting average could be, we want to assume the highest numerator (hits of 3) and the lowest denominator (at bats of 4): 3/4 = 0.75.
  5. Combining these answers yields the correct answer C: between 0.33 and 0.75.
GMAT Classic Mock Test - 6 - Question 7
Save

Let f(x) = x2 + bx + c. If f(1) = 0 and f(-4) = 0, then f(x) crosses the y-axis at what y-coordinate?
Detailed Solution for GMAT Classic Mock Test - 6 - Question 7
  1. This problem requires working backward from solutions to a quadratic equation to the equation itself.
    Instead of factoring a quadratic equation to solve it (the process many questions require), this question requires you to go the other way—from solutions to factors.
    f(x) = x2 + bx + c = 0
  2. The key to unlocking this problem is recognizing that if f(a) = 0 and f(x) is a quadratic equation in the form x2 + bx + c = 0, (x – a) is a factor of the equation.
    (x + d)(x + e) = x2 + dex + de = 0
  3. If this past step does not make sense immediately, take a look at a few examples and allow them to convince you of this truth.
    x2 + 3x - 4 = 0
    (x - 1)(x + 4)
    Solutions: f(1) = 0 or f(-4) = 0

    x2 -9x + 20 = 0
    (x – 4)(x – 5)
    Solutions: f(4) = 0 or f(5) = 0
  4. Following this same principle, you know that since f(1) = 0 and f(-4) = 0, (x – 1) and (x + 4) are factors.
    (x – 1)(x + 4) = 0
  5. Multiply these factors together to form a quadratic equation.
    (x – 1)(x + 4) = 0
    x2 – x + 4x – 4 = 0
    x2 + 3x – 4 = 0
  6. For any quadratic equation in the form ax2 + bx + c = 0, the y-intercept (i.e., the place where the equation crosses the y-axis) is c.
    Even if you did not know this, you could still find the y-axis. The line will cross the y-axis where x = 0.
    f(0) = (0)2 + 3(0) – 4 = -4
  7. Y-Intercept is -4
GMAT Classic Mock Test - 6 - Question 8
Save

Superior Security recently discovered a computer on its network had been hacked. The computer password contained 16 characters (including only numbers and letters). What is the probability that the password to Superior’s hacked computer was correctly guessed on the first try? (Assume that the hacker knew the password contained 16 characters, comprised only of numbers and both lower-case and upper-case letters.)
Detailed Solution for GMAT Classic Mock Test - 6 - Question 8
  1. The probability of guessing correctly on the first try is 1 divided by the number of pass permutations (i.e., unique arrangements of passwords). For example, if there were four possible password combinations, the probability of guessing the password correctly on the first try would be 1/4
  2. For each of the 16 characters that form the password, the possible characters include: 26 lower case characters, 26 upper case characters, and 10 digits. So, for each character in the password, there are 62 possible characters.
  3. Since there are 16 characters in the password and each character could be one of 62 possibilities, there are a total of 6216 unique password permutations (i.e., there are 6216 different possible passwords, only one of which is the correct password). So, the probability of guessing the password on the first try is 1/6216.
GMAT Classic Mock Test - 6 - Question 9
Save

The average (arithmetic mean) of a and b is 90; the average (arithmetic mean) of a and c is 150; what is the value of (b-c)/2?
Detailed Solution for GMAT Classic Mock Test - 6 - Question 9
  1. Translate the question into algebra, using the formula that the average equals the sum of the terms divided by the number of terms.
    90 = (a + b)/2
    Multiply by 2: 180 = a + b

    150 = (a + c)/2
    Multiply by 2: 300 = a + c
  2. At this point, there are two ways to manipulate the algebra.
  3. Method 1
    1. Line up the two equations so that you can subtract them.
      Equation 1: a+b = 180
      Equation 2: a + c = 300
    2. Notice that the equations are lined up such that if you subtract them, you end up with b-c on the left and a number on the right. Since you are trying to find (b - c)/2, this setup will get you most of the way to the answer.
    3. Subtract the two equations:
      Equation 1: a + b = 180
      Equation 2: a+c = 300
      Equation 1 - 2: a - a + b - c = 180 - 300 = -120
      Equation 1 - 2 (cont.): b-c = -120
    4. With b - c = -120, if you divide by two, you arrive at the equation that you are being asked for:
      (b - c)/2 = -120/2 = -60
  4. Method 2
    1. Since the question asks for the value of (b-c)/2, solve the two equations for the variable a so that they can be combined.
      a = 180 – b
      a = 300 – c
    2. Combine the two equations by setting them equal to each other (since a = a) and manipulate them such that (b - c)/2 is on one side of the equation and a number is on the other.
      180 – b = 300 – c
      180 – 300 = b – c
      -120 = b-c
      -60 = (b – c)/2
GMAT Classic Mock Test - 6 - Question 10
Save

f(x) = x2 + 4x + k = 12; f(-6) = 0; if k is a constant and n is the number for which f(n) = 0, what is the value of n?
Detailed Solution for GMAT Classic Mock Test - 6 - Question 10
  1. There are two main approaches you can take to solving this problem. You can either solve for k and turn this problem into a simple factoring problem or you can ignore k and reverse factor.
  2. Method 1: Solve for K.
    1. f(x) = x2 + 4x + k = 12
      f(x) = x2 + 4x + k - 12 = 0 (subtract 12)
    2. Plug in x = -6 knowing that the value of f(x) must equal zero since f(-6)=0.
      f(-6) = (-6)2 + 4(-6) + k - 12 = 0
      36 - 24 + k - 12 = 0
      0 - k = 0 → k = 0
    3. The equation is now:
      f(x) = x2 + 4x + 0 - 12 = 0
      f(x) = x2 + 4x - 12 = 0
    4. By factoring: x2 + 4x - 12 = 0 equals:
      (x + 6)(x + n) Note: x + 6 is from f(-6)=0
    5. Since we need two numbers that add to +4 and multiply to -12, we know that +6 and -2 work. Consequently, (x - 2) is a factor and therefore, f(+2)=0, so n = 2.
  3. Method 2: Ignore K.
    1. A crucial insight in unlocking this problem is recognizing that if f(a) = 0 and f(x) is a quadratic equation in the form x2 + bx + c = 0, (x – a) is a factor of the equation. In order to get the equation into quadratic form, subtract 12.
      f(x) = x2 + 4x + k = 12
      f(x) = x2 + 4x + k – 12 = 0
    2. Since f(-6) = 0, (x + 6) is a factor.
    3. It is important to remember how factoring works. Specifically, remember the following:
      (x + d)(x + e) = x2 + dex + de = 0
      So: (x + 6)(x + a) = x2 + 4x + (k – 12)
    4. With this in mind, you know that 6 + a = 4. So, a = -2 and therefore, (x - 2) is the other factor of the quadratic. So, f(2) = 0 and n = 2.
  4. Answer B is correct.
GMAT Classic Mock Test - 6 - Question 11
Save

What is the value of the following fraction:
Detailed Solution for GMAT Classic Mock Test - 6 - Question 11
  1. Since 26 = 13(2), 263 = (13 x 2)3 = (13)3  x  23
  2. The numerator of the fraction can be simplified:
    263 + 133
    (13 x 2)3 + (13)3
    (13)3 x (2)3 + (13)3
  3. Factor the common term of (13)3 out:
    (13)3 x (2)3 + (13)3
    (13)3(23 + 1)
  4. Using the powers of exponents, you can make the following simplifications:
  5. Continue the simplification:
  6. The correct answer is D.
GMAT Classic Mock Test - 6 - Question 12
Save

A computer has three hard-drives; the smallest and largest hard-drives account for 25 and 45 percent of the total storage space on the computer, respectively; due to a catastrophic error, the largest hard-drive lost approximately 22% of its storage space; after this error, the hard drive that was originally the second largest accounts for approximately what percent of the total hard-drive space on the reduced computer?
Detailed Solution for GMAT Classic Mock Test - 6 - Question 12
  1. Since there are only three hard drives and these account for 100% of the space on the computer, you can write the following equation:
    (Smallest Hard Drive) + (Medium Hard Drive) + (Large Hard Drive) = 100%
    25% + (Medium Hard Drive) + 45% = 100%
  2. You now know the size of the medium hard drive:
    (Medium Hard Drive) = 30%
  3. If the largest hard-drive lost approximately 22% of its storage space, it now accounts for (1-.22)(.45) = .351 or 35.1% of the old total space.
  4. You can now find what percent of the total hard-drive space the second largest hard drive accounts for:
    = (Drive Originally 2nd Largest) / (New Total Drive Space)
    = 30%/(35.1% + 25% + 30%) = 30%/90% = ~ 33%
  5. If the concept of manipulating and dividing percents throws you off, this is an excellent problem to pick numbers on. Simply let the percents be actual hard-drive space. In other words, set the total hard drive space to be 100GB. Then, the smallest hard-drive is 25GB, the medium hard-drive is 30GB, and the largest is 45GB. After the largest shrinks by 22%, it is now 45 x (1-.22) = 35GB. So, the reduced hard drive is 25 + 30 + 35 = 90GB and the second largest hard drive is 30GB/90GB = 33%.
GMAT Classic Mock Test - 6 - Question 13
Save

Chef Martha is preparing a pie for a friend's birthday. How much more of substance X does she need than substance Y?
(1) Martha needs 10 cups of substance X
(2) Martha needs the substances W, X, Y, and Z in the ratio: 15:5:2:1 and she needs 4 cups of substance Y
Detailed Solution for GMAT Classic Mock Test - 6 - Question 13
  1. The phrase "how much more of substance X does she need than substance Y" can be translated into algebra as: X - Y
  2. Evaluate Statement (1) alone.
    1. Although X = 10, there is no information about Y. Consequently, we cannot determine the value of X - Y
    2. Statement (1) is NOT SUFFICIENT.
  3. Evaluate Statement (2) alone.
    1. Y = 4 and the ratio of X:Y = 5:2. Consequently, X = 10 and X - Y = 10 - 4 = 6
    2. Statement (2) is SUFFICIENT.
  4. Since Statement (1) alone is NOT SUFFICIENT but Statement (2) alone is SUFFICIENT, answer B is correct.
GMAT Classic Mock Test - 6 - Question 14
Save

How many computers did Michael, a salesman for the computer company Digital Electronics Labs, sell this past year that had more than 4GB of RAM and the Microsoft Windows Vista operating system? (Michael sold no computers with exactly 4GB of RAM)
(1) 40% of the 200 total computers that Michael sold had Vista and less than 4GB of RAM; these computers represent 80% of the total computers that Michael sold with Vista.
(2) 50% of the 200 total computers that Michael sold had Vista; Of the computers that Michael sold without Vista, half had more than 4GB of ram while the other half had less than 4GB of RAM.
Detailed Solution for GMAT Classic Mock Test - 6 - Question 14
  1. Evaluate Statement (1) alone.
    1. 40% of 200 is 80, so Michael sold 80 computers with Vista and less than 4GB of RAM.
    2. These 80 computers represent 80% of the total computers Michael sold with Vista, so Michael sold a total of 100(=80/80%) computers with Vista.
    3. Vistatotal = Vista<4GB + Vista>4GB
      100 = 80 + Vista>4GB
      Vista>4GB = 20
    4. Statement (1) alone is SUFFICIENT.
    5. Note: At this point, you should not continue making calculations since you have determined sufficiency. However, to be complete, we included additional information you can deduce:
      VistaTotal + NoVistaTotal = Total
      100 + NoVistaTotal = 200
      NoVistaTotal = 100 and Michael sold a total of 100 computers without Vista.
  2. Evaluate Statement (2) alone.
    1. "50% of the 200 total computers that Michael sold had Vista" means that 100 computers had Vista. Consequently, 100 computers Michael sold did not have Vista.
    2. "Of the computers that Michael sold without Vista, half had more than 4GB of RAM while the other half had less than 4GB of RAM" means that one-half of the 100 computers without Vista (i.e., 50) had more than 4GB of RAM while the other half (i.e., 50) had less than 4GB of RAM.
    3. We cannot determine the number of computers sold both with Vista and more than 4GB of RAM, so Statement (2) is NOT SUFFICIENT.
    4. Statement (2) alone is NOT SUFFICIENT.
  3. Since Statement (1) alone is SUFFICIENT and Statement (2) alone is NOT SUFFICIENT, answer A is correct.
GMAT Classic Mock Test - 6 - Question 15
Save

x is a positive integer; is x + 17, 283 odd?
(1) x - 192, 489, 358, 935 is odd
(2) x/4 is not an even integer
Detailed Solution for GMAT Classic Mock Test - 6 - Question 15
  1. Before evaluating Statements (1) and (2), it is extremely helpful to keep in mind that an odd number is the result of a sum of numbers with unlike parity. In other words: even + odd = odd. Since 17,283 is odd, the only way x + 17,283 will be odd is if x is even. Consequently, the simplified version of the question is: is x even?
  2. Evaluate Statement (1) alone.
    1. Statement (1) says that x - 192,489,358,935 is odd. Since there is only one way for a difference to be odd (i.e., if the parity of the numbers is different), Statement (1) implies that x is even (otherwise, if x were odd, x - 192,489,358,935 would be even). Since Statement (1) gives the parity of x, it is SUFFICIENT.
    2. Statement (1) alone is SUFFICIENT.
  3. Evaluate Statement (2) alone.
    1. Statement (2) says that x/4 is not an even integer. It is important to note that this does not mean that x cannot be even (e.g., 6 is even yet 6/4 is not an even integer). Possible values of x include 2, 3, 6, 10, 11.
    2. As this list indicates, there is no definitive information about the parity of x (e.g., 11 is odd and 10 is even). Consequently, Statement (2) is NOT SUFFICIENT.
    3. Statement (2) alone is NOT SUFFICIENT.
  4. Since Statement (1) alone is SUFFICIENT and Statement (2) alone is NOT SUFFICIENT, answer A is correct.
GMAT Classic Mock Test - 6 - Question 16
Save

If n is a positive integer, is n + 2 > z?
(1) z2 > n
(2) z – n < 0
Detailed Solution for GMAT Classic Mock Test - 6 - Question 16
  1. Evaluate Statement (1) alone.
    1. The smallest possible value of n is 1 since n is a positive integer and the smallest positive integer is 1
    2. You know that z2 > 1, which is the smallest possible value of n. Possible values of z include any number whose absolute value is greater than 1. This does not provide enough information to answer the question definitively. Consider the following examples.
      If z = -10 and n = 1, two values that are permissible since (-10)2 > 1, then the answer to the original question is yes since 1 + 2 > -10.
      However, if z = 10 and n = 1, two values that are permissible since (10)2 > 1, then the answer to the original question is no since 1 + 2 is not greater than 10.
      Statement (1) is NOT SUFFICIENT.
  2. Evaluate Statement (2) alone.
    1. Statement (2) can be re-arranged:
      z - n < 0
      z < n
      Stated Differently: n > z
      Since n is greater than z, n + 2 will definitely be greater than z because n is a positive integer and it will only become larger.
      In other words, let z = (a number less than n). You can be sure that n + 2 will definitely be greater than (a number less than n).
      Statement (2) is SUFFICIENT.
  3. Since Statement (1) alone is NOT SUFFICIENT and Statement (2) alone is SUFFICIENT, answer B is correct.
GMAT Classic Mock Test - 6 - Question 17
Save

Peter can drive to work via the expressway or via the backroads, which is a less delay-prone route to work. What is the difference in the time Peter would spend driving to work via the expressway versus the backroads?

(1) Peter always drives 60mph, regardless of which route he takes; it takes Peter an hour to drive round-trip to and from work using the backroads

(2) If Peter travels to and from work on the expressway, he spends a total of 2/3 of an hour traveling
Detailed Solution for GMAT Classic Mock Test - 6 - Question 17
  1. Since this is a distance-rate-time problem, begin with the core equation:
    Distance = Rate(Time)
    Note that there are two distance equations, one for traveling the expressway and the other for traveling the backroads.
    Distanceexpress = Rateexpress(Timeexpress)
    Distancebackroad = Ratebackroad(Timebackroad)
  2. In order to answer the question, you need to find the value of:
    Timeexpress - Timebackroad
  3. Evaluate Statement (1) alone.
    1. Statement (1) says Rateexpress = Ratebackroad = 60 mph.
    2. Statement (1) also says that 2(Timebackroad) = 1 hour
      (Time is multiplied by 2 because the statement gives the time "to drive round-trip to and from work.")
      Timebackroad = 1/2 hour.
    3. Filling in all the information, you have the following:
      Distanceexpress = 60(Timeexpress)
      Distancebackroad = 60mph((1/2) hour) = 30 miles
    4. Without information concerning the distance or time to travel on the expressway, you cannot solve for Timeexpress. Consequently, Statement (1) is NOT SUFFICIENT.
  4. Evaluate Statement (2) alone.
    1. Statement (2) says that 2(Distanceexpress) = Rateexpress((2/3) of an hour)
      (Note that the distance is multiplied by two because Peter travels twice the distance when he goes "to and from work".)
      So, Timeexpress = 1/3 of an hour.
    2. Fill in the information that is known:
      Distanceexpress = Rateexpress(1/3 of an hour)
      Without any information about Timebackroad, you cannot determine Timeexpress - Timebackroad. Statement (2) is NOT SUFFICIENT.
  5. Evaluate Statements (1) and (2) together.
    1. Putting Statements (1) and (2) together, you know Timebackroad from Statement (1) and you know Timeexpress from Statement (2).
    2. So, Timeexpress - Timebackroad = 1/3hour - 1/2hour or 20 minutes - 30 minutes = 10 minutes or 1/6 of an hour. Statements (1) and (2) together are SUFFICIENT.
  6. Since Statement (1) alone is NOT SUFFICIENT and Statement (2) alone is NOT SUFFICIENT yet Statements (1) and (2), when taken together, are SUFFICIENT, answer C is correct.
GMAT Classic Mock Test - 6 - Question 18
Save

a, b, c, and d are integers; abcd≠0; what is the value of cd?

(1) c/b = 2/d

(2) b3a4c = 27a4c
Detailed Solution for GMAT Classic Mock Test - 6 - Question 18
  1. Evaluate Statement (1) alone.
    1. Cross-multiply:
      c/b = 2/d
      cd = 2b
    2. Since b could be any integer, the value of cd cannot be definitively determined. For example, if b = 2, then cd = 4. However, if b = 3, then cd = 6.
    3. Since we cannot determine the value of cd, Statement (1) is NOT SUFFICIENT.
  2. Evaluate Statement (2) alone.
    1. Simplify by dividing common terms:
      b3a4c = 27a4c
      b3 = 27; (divided by a4c)
      b = 3
    2. By knowing that b = 3, there is no information about the value of cd. (Do not make the mistake of importing the information from Statement (1) into your evaluation of Statement (2)).
    3. Since we cannot determine the value of cd, Statement (2) is NOT SUFFICIENT.
  3. Evaluate Statements (1) and (2) together.
    1. Combining Statements (1) and (2), you know that b = 3 and cd = 2b.
    2. By plugging b = 3 into cd=2b, you know that cd = 2(3) = 6. Combining Statements (1) and (2), you can find a definitive value of cd.
  4. Statements (1) and (2), when taken together, are SUFFICIENT. Answer C is correct.
GMAT Classic Mock Test - 6 - Question 19
Save

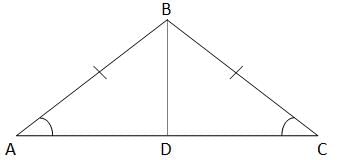
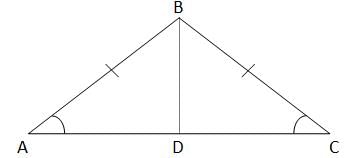
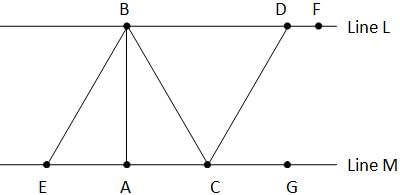
If angle ABC is 30 degrees, what is the area of triangle BCE?

(1) Angle CDF is 120 degrees, lines L and M are parallel, and AC = 6, BC = 12, and EC = 2AC

(2) Angle DCG is 60 degrees, angle CDG is 30 degrees, angle FDG = 90, and GC = 6, CD = 12 and EC = 12
Detailed Solution for GMAT Classic Mock Test - 6 - Question 19
  1. Even though lines L and M look parallel and angle BAC looks like a right angle, you cannot make these assumptions.
  2. The formula for the area of a triangle is .5bh
  3. Evaluate Statement (1) alone.
    1. Since EC = 2AC, EA = CA, EC = 2(6) = 12 and line AB is an angle bisector of angle EBC. This means that angle ABC = angle ABE. Since we know that angle ABC = 30, we know that angle ABE = 30. Further, since lines L and M are parallel, we know that line AB is perpendicular to line EC, meaning angle BAC is 90.
    2. Since all the interior angles of a triangle must sum to 180:
      angle ABC + angle BCA + angle BAC = 180
      30 + angle BCA + 90 = 180
      angle BCA = 60
    3. Since all the interior angles of a triangle must sum to 180:
      angle BCA + angle ABC + angle ABE + angle AEB = 180
      60 + 30 + 30 + angle AEB = 180
      angle AEB = 60
    4. This means that triangle BCA is an equilateral triangle.
    5. To find the area of triangle BCE, we need the base (= 12 from above) and the height, i.e., line AB. Since we know BC and AC and triangle ABC is a right triangle, we can use the Pythagorean theorem on triangle ABC to find the length of AB.
      62 + (AB)2 = 122
      AB2 = 144 - 36 = 108
      AB = 1081/2
    6. Area = .5bh
      Area = .5(12)(1081/2) = 6*1081/2
    7. Statement (1) is SUFFICIENT
  4. Evaluate Statement (2) alone.
    1. The sum of the interior angles of any triangle must be 180 degrees.
      DCG + GDC + CGD = 180
      60 + 30 + CGD = 180
      CGD = 90
      Triangle CGD is a right triangle.
    2. Using the Pythagorean theorem, DG = 1081/2
      (CG)2 + (DG)2 = (CD)2
      62 + (DG)2 = 122
      DG = 1081/2
    3. At this point, it may be tempting to use DG = 1081/2 as the height of the triangle BCE, assuming that lines AB and DG are parallel and therefore AB = 1081/2 is the height of triangle BCE. However, we must show two things before we can use AB = 1081/2 as the height of triangle BCE: (1) lines L and M are parallel and (2) AB is the height of triangle BCE (i.e., angle BAC is 90 degrees).
    4. Lines L and M must be parallel since angles FDG and CGD are equal and these two angles are alternate interior angles formed by cutting two lines with a transversal. If two alternate interior angles are equal, we know that the two lines that form the angles (lines L and M) when cut by a transversal (line DG) must be parallel.
    5. Since lines L and M are parallel, DG = the height of triangle BCE = 1081/2. Note that it is not essential to know whether AB is the height of triangle BCE. It is sufficient to know that the height is 1081/2. To reiterate, we know that the height is 8 since the height of BCE is parallel to line DG, which is 1081/2.
    6. Since we know both the height (1081/2) and the base (CE = 12) of triangle BCE, we know that the area is: .5*12*1081/2 = 6*1081/2
    7. Statement (2) alone is SUFFICIENT.
  5. Since Statement (1) alone is SUFFICIENT and Statement (2) alone is SUFFICIENT, answer D is correct.
GMAT Classic Mock Test - 6 - Question 20
Save

If both x and y are positive integers less than 100 and greater than 10, is the sum x + y a multiple of 11?

(1) x - y is a multiple of 22

(2) The tens digit and the units digit of x are the same; the tens digit and the units digit of y are the same
Detailed Solution for GMAT Classic Mock Test - 6 - Question 20
  1. If both x and y are multiples of 11, then both x + y and x - y will be multiples of 11. In other words, if two numbers have a common divisor, their sum and difference retain that divisor.
    In case this is hard to conceptualize, consider the following examples:
    42 - 18 {both numbers share a common factor of 6}
    =(6 x 7) - (6 x 3)
    =6(7 - 3)
    =6(4)
    =24 {which is a multiple of 6}

    49 + 14 {both numbers share a common factor of 7}
    =(7 x 7) + (7 x 2)
    =7(7+2)
    =7*9
    =63 {which is a multiple of 7}
  2. However, if x and y are not both multiples of 11, it is possible that x - y is a multiple of 11 while x + y is not a multiple of 11. For example:
    68 - 46 = 22 but 68 + 46 = 114, which is not divisible by 11.
    The reason x - y is a multiple of 11 but not x + y is that, in this case, x and y are not individually multiples of 11.
  3. Evaluate Statement (1) alone.
    1. Since x-y is a multiple of 22, x-y is a multiple of 11 and of 2 because 22 = 11 x 2
    2. If both x and y are multiples of 11, the sum x + y will also be a multiple of 11. Consider the following examples:
      44 - 22 = 22 {which is a multiple of 11 and of 22}
      44 + 22 = 66 {which is a multiple of 11 and of 22}
      88 - 66 = 22 {which is a multiple of 11 and of 22}
      88 + 66 = 154 {which is a multiple of 11 and of 22}
    3. However, if x and y are not individually divisible by 11, it is possible that x - y is a multiple of 22 (and 11) while x + y is not a multiple of 11. For example:
      78 - 56 = 22 but 78 + 56 = 134 is not a multiple of 11.
    4. Statement (1) alone is NOT SUFFICIENT.
  4. Evaluate Statement (2) alone.
    1. Since the tens digit and the units digit of x are the same, the range of possible values for x includes:
      11, 22, 33, 44, 55, 66, 77, 88, 99
      Since each of these values is a multiple of 11, x must be a multiple of 11.
    2. Since the tens digit and the units digit of y are the same, the range of possible values for y includes:
      11, 22, 33, 44, 55, 66, 77, 88, 99
      Since each of these values is a multiple of 11, y must be a multiple of 11.
    3. As demonstrated above, if both x and y are a multiple of 11, we know that both x + y and x - y will be a multiple of 11.
    4. Statement (2) alone is SUFFICIENT.
  5. Since Statement (1) alone is NOT SUFFICIENT and Statement (2) alone is SUFFICIENT, answer B is correct.
GMAT Classic Mock Test - 6 - Question 21
Save

If b is prime and the symbol # represents one of the following operations: addition, subtraction, multiplication, or division, is the value of b # 2 even or odd?
1. (b # 1) # 2 = 5
2. 4 # b = 3 # (1 # b) and b is even
Detailed Solution for GMAT Classic Mock Test - 6 - Question 21
  1. This problem deals with the properties of prime numbers. Keep in mind that 1 is not a prime number and that 2 is the only even prime number.
  2. Evaluate Statement (1) alone.
    1. Try each of the operations in turn. First, try addition:
      (b + 1) + 2 = 5
      Solve for b.
      b = 2.
      Under addition, b = 2, which is a prime number; therefore addition is a possibility for the operator.
    2. Next, try subtraction.
      (b - 1) - 2 = 5
      Solve for b.
      b = 8
      But b = 8 is not prime, therefore operator cannot represent subtraction.
    3. Next, try multiplication.
      (b x 1)  x 2 = 5
      Solve for b.
      b = 5/2
      But b = 5/2 is not prime, therefore operator cannot represent multiplication.
    4. Finally, try division.
      (b / 1) / 2 = 5
      Solve for b.
      b = 10
      But b = 10 is not prime, therefore operator cannot represent division.
    5. Since addition is the only operation for which b is prime, # must represent addition. In this case, b = 2 and the value of b # 2 is 4, which is even.
    6. Statement (1) is SUFFICIENT.
  3. Evaluate Statement (2) alone.
    1. Try each of the operations in turn. First, try addition:
      4 + b = 3 + (1 + b)
      Subtract 4 from each side.
      b = b
      While this is true, it does not give any information about the value of b. However, addition is still a possible operation.
    2. Next, try subtraction:
      4 - b = 3 - (1 - b)
      Solve for b.
      b = 1
      In this case, b = 1 is not a prime number, so subtraction is not a possible operation.
    3. Next, try multiplication:
      4 x b = 3 x (1 x b)
      Simplify.
      4b = 3b
      The only value for which this holds true is b = 0, which is not a prime number. Therefore, multiplication is not a possible operation.
    4. Finally, try division:
      4 / b = 3 / (1 / b)
      Multiply both sides by (1 / b)
      4 / b2 = 3
      Solve for b2.
      b2 = 4/3
      Which means that b = sqrt(4/3) or b = -sqrt(4/3). Neither of these is prime, so division is not a possible operation.
    5. The symbol # must represent addition, since this is the only possible operation. By Statement (2), b is even, but b is still prime. Since 2 is the only even prime number, b must be 2. In this case, the value of b # 2 is even because an even number plus 2 is still an even number.
    6. Statement (2) is SUFFICIENT.
  4. Since Statement (1) alone is SUFFICIENT and Statement (2) alone is SUFFICIENT, answer D is correct.
GMAT Classic Mock Test - 6 - Question 22
Save

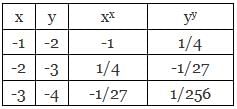
If x and y are both integers, which is larger, xx or yy?

  1. x = y + 1
  2. xy > x and x is positive.
Detailed Solution for GMAT Classic Mock Test - 6 - Question 22
  1. The problem deals with properties of exponents. Analyzing the different cases where x is positive and y is positive, for example, is the key to this problem.
  2. Evaluate Statement (1) alone.
    1. Since x = y + 1, substitute for x in xx.
      xx = (y + 1)(y + 1)
    2. Since x is one number larger than y, it may appear that xx must be larger than yy. However, consider the table below.
    3. When x = -1 and y = -2, xx is smaller. However, when x = -2 and y = -3, yy is smaller. Whether xx or yy is larger depends on the values of x and y.
    4. Statement (1) is NOT SUFFICIENT.
  3. Evaluate Statement (2) alone.
    1. Given the inequality from Statement (2),
      xy > x
      Divide both sides by x.
      x(y - 1) > 1
    2. First consider this inequality when y = 1. Then x(y - 1) = x(1 - 1) = 1. But this violates the inequality because it is not true that x(1 - 1) > 1. Therefore, y may not be 1.
    3. Next consider the case where y < 1. Then x(y - 1) = x-k, where -k is some negative number. And x-k = 1 / xk, which is less than 1 no matter the value of x; this violates the inequality, too, since x(y - 1) is supposed to be greater than 1. For example, if y = -3 and x = 2, then x(y - 1) = 2(-3 - 1) = 1 / 24 = 1/8, which is less than 1.
    4. Since it cannot be that y = 1 or y < 1, the only option that remains is y > 1. From this conclusion and the information given in Statement (2), we conclude that x > 0 and y > 1. However, this is not enough information to determine whether xx or yy is larger. For example, it could be that x = 4 and y = 6; in this case, yy would be larger. It could be that x = 7 and y = 3; in this case, xx would be larger.
    5. Statement (2) is NOT SUFFICIENT.
  4. Evaluate Statement (1) and (2) together.
    1. The conclusion reached in examining Statement (2) was that y > 1 and x > 0. Combine this with Statement (1), which says that x is one number larger than y. Thus, xx will always be larger than yy. For example, if y = 2, then x = 3; yy = 22 = 4 and xx = 33 = 27.
    2. Statement (1) and (2) together are SUFFICIENT.
  5. Since Statement (1) alone is NOT SUFFICIENT and Statement (2) alone is NOT SUFFICIENT yet Statements (1) and (2), when taken together, are SUFFICIENT, answer C is correct.
GMAT Classic Mock Test - 6 - Question 23
Save

A: x2 + 6x - 40 = 0
B: x2 + kx + j = 0
Which is larger, the sum of the roots of equation A or the sum of the roots of equation B?

  1. j = k
  2. k is negative
Detailed Solution for GMAT Classic Mock Test - 6 - Question 23
  1. This problem combines the quadratic formula with properties of positive and negative numbers. First, find the sum of the roots in equation A using the quadratic formula or factoring.
    Using the quadratic formula:
    x = (-6 + sqrt(36 - 4(1)(-40))) / 2 and (-6 - sqrt(36 - 4(1)(-40))) / 2 are the roots.

    Using factoring:
    x2 + 6x - 40 = 0
    (x + 10)(x - 4) = 0
    x = -10, 4
  2. To find the sum, these two roots will be added. Notice that one root contains +sqrt(36 + 160) and the other contains -sqrt(36 + 160). When these two terms are added, they equal zero. Thus, the only terms left in the sum are -6/2 and -6/2. Add these together to find the sum of the roots: -6/2 + (-6/2) = -6. Notice that the sum of the roots equals -b, where b is the coefficient of the x term.
  3. In fact, in any sum of quadratic roots, the +sqrt(...) and -sqrt(...) terms will cancel. Therefore, for any quadratic equation the sum of the roots is -b, where b is the coefficient of the x term (ax2 + bx + c = 0). This fact will simplify the problem greatly.
  4. Evaluate Statement (1) alone.
    1. The sum of the roots for equation A was found to be -6. Using the fact demonstrated above, the sum of the roots of equation B is -k. Statement (1) says that that j = k, which means that the sum of the roots of equation B is -k = -j.
    2. However, nothing is known about j and k. It could be that j = -7, in which case the sum of the roots of B is -(-7) = 7, which is larger than the sum of the roots of A. However, it could be that j = 9, in which case the sum of the roots of B is -(9) = -9, which is smaller than the sum of the roots of A. It cannot be determined which sum is larger.
    3. Note: We cannot assume that j and k are integers as the problem does not state this. If we knew they were integers, then j = k = 2 since this is the only way for j to equal k in x2 + jx + k = 0, and we could solve the problem.
    4. Statement (1) is NOT SUFFICIENT.
  5. Evaluate Statement (2) alone.
    1. If k is negative, then the sum of the roots of B is -k, which is the negative of a negative number, making the sum positive. And since this sum is positive, it is larger than the sum of the roots of A, which is -6.
    2. Statement (2) is SUFFICIENT.
  6. Since Statement (1) alone is NOT SUFFICIENT and Statement (2) alone is SUFFICIENT, answer B is correct.
GMAT Classic Mock Test - 6 - Question 24
Save

Given that A = 3y + 8x, B = 3y - 8x, C = 4y + 6x, and D = 4y - 6x, what is the value of x*y?

  1. AB + CD = -275
  2. AD - BC = 420
Detailed Solution for GMAT Classic Mock Test - 6 - Question 24
  1. This problem deals with polynomials and factoring, as well as simultaneous equations with two variables. Factoring or expanding where necessary will help greatly in solving this problem.
  2. Evaluate Statement (1) alone.
    1. First, multiply A and B, then C and D.
      AB = (3y + 8x)(3y - 8x) = 9y2 - 64x2
      CD = (4y + 6x)(4y - 6x) = 16y2 - 36x2
    2. Now add AB and CD.
      AB + CD = 25y2 - 100x2
      Factor a 25 out of the right side of the equation.
      AB + CD = 25(y2 - 4x2)
      Notice that the polynomial on the right side can be factored.
      AB + CD = 25(y + 2x)(y - 2x)
    3. Since AB + CD = -275, substitute this value into the equation.
      -275 = 25(y + 2x)(y - 2x)
      Divide both sides by 25.
      -11 = (y + 2x)(y - 2x)
    4. Let P = y + 2x and Q = y - 2x. There are only four ways that -11 can be the product of the two numbers P and Q: P = -1 and Q = 11, or P = -11 and Q = 1, or P = 1 and Q = -11, or P = 11 and Q = -1. Examine the first two possibilities.
    5. First, P = -1 and Q = 11. Write out P and Q fully.
      P = y + 2x = -1
      Q = y - 2x = 11
      Using linear combination, add both sides of the two equations together.
      2y = 10
      Which means that y = 5. Plug y = 5 back into either equation and get x = -3.
    6. Secondly, P = -11 and Q = 1. Write out P and Q fully.
      P = y + 2x = -11
      Q = y - 2x = 1
      Using linear combination, add both sides of the two equations together.
      2y = -10
      Which means that y = -5. Plug y = -5 back into either equation and get x = -3.
    7. In the first case, y = 5 and x = -3, which means that x*y = -15. However, in the second case, when y = -5 and x = -3, x*y = +15. Therefore it is not possible to determine the value of x*y since the sign cannot be determined.
    8. Statement (1) is NOT SUFFICIENT.
  3. Evaluate Statement (2) alone.
    1. First, multiply A and D, then B and C.
      AD = (3y + 8x)(4y - 6x) = 12y2 + 14xy - 48x2
      BC = (3y - 8x)(4y + 6x) = 12y2 - 14xy - 48x2
    2. Now subtract BC from AD; almost all the terms cancel out.
      AD - BC = 14xy - (-14xy) = 28xy
      Since AD - BC = 420, substitute this value into the equation.
      420 = 28xy.
      Divide both sides by 28.
      xy = 15
    3. Statement (2) is SUFFICIENT.
  4. Since Statement (1) alone is NOT SUFFICIENT and Statement (2) alone is SUFFICIENT, answer B is correct.
GMAT Classic Mock Test - 6 - Question 25
Save

After a long career, John C. Walden is retiring. If there are 25 associates who contribute equally to a parting gift for John in an amount that is an integer, what is the total value of the parting gift?

  1. If four associates were fired for underperformance, the total value of the parting gift would have decreased by $200
  2. The value of the parting gift is greater than $1,225 and less than $1,275
Detailed Solution for GMAT Classic Mock Test - 6 - Question 25
  1. Simplify the question by translating it into algebra.
    Let P = the total value of John's parting gift
    Let E = the amount each associate contributed
    Let N = the number of associates
    P = NE = 25E
  2. With this algebraic equation, if you find the value of either P or E, you will know the total value of the parting gift.
  3. Evaluate Statement (1) alone.
    1. Two common ways to evaluate Statement (1) alone:
  4. Statement 1: Method 1
    1. Since the question stated that each person contributed equally, if losing four associates decreased the total value of the parting gift by $200, then the value of each associate's contribution was $50 (=$200/4).
    2. Consequently, P = 25E = 25(50) = $1,250.
  5. Statement 1: Method 2
    1. If four associates leave, there are N - 4 = 25 - 4 = 21 associates.
    2. If the value of the parting gift decreases by $200, its new value will be P - 200.
    3. Taken together, Statement (1) can be translated:
      P - 200 = 21E
      P = 21E + 200
    4. You now have two unique equations and two variables, which means that Statement (1) is SUFFICIENT.
    5. Although you should not spend time finding the solution on the test, here is the solution.
      Equation 1: P = 21E + 200
      Equation 2: P = 25E
      P = P
      25E = 21E + 200
      4E = 200
      E = $50
    6. P = NE = 25E = 25($50) = $1250
  6. Evaluate Statement (2) alone.
    1. Statement (2) says that $1,225 < P < $1,275. It is crucial to remember that the question stated that "25 associates contribute equally to a parting gift for John in an amount that is an integer." In other words P / 25 must be an integer. Stated differently, P must be a multiple of 25.
    2. There is only one multiple of 25 between 1,225 and 1,275. That number is $1,250. Since there is only one possible value for P, Statement (2) is SUFFICIENT.
  7. Since Statement (1) alone is SUFFICIENT and Statement (2) alone is SUFFICIENT, answer D is correct.
GMAT Classic Mock Test - 6 - Question 26
Save

f n and k are integers and (-2)n5 > 0, is k37 < 0?

  1. (nk)z > 0, where z is an integer that is not divisible by two
  2. k < n
Detailed Solution for GMAT Classic Mock Test - 6 - Question 26
  1. It is important to begin by simplifying the question.
    Since k is raised to an odd power, k37 will always be less than 0 if k is less than 0. Likewise, k37 will always be greater than 0 if k is greater than 0.
    So, the question can be simplified to: is k < 0?
    k(odd integer) < 0 if k < 0
    k(odd integer) > 0 if k > 0
  2. The question can be simplified even more. Since (-2)(negative number) > 0 and (-2)(positive number) < 0, you know n5 is a negative number. This means that n < 0. If n were greater than 0, the statement (-2)n5 > 0 would never be true.
  3. Summarizing in algebra:
    (-2)(negative number) > 0
    (-2)(positive number) < 0
    (-2)(n5) > 0
    n5 < 0
    Therefore: n < 0
  4. The fully simplified question is: "if n and k are integers and n < 0, is k < 0?"
  5. Evaluate Statement (1) alone.
    1. By saying that "z is an integer that is not divisible by 2," Statement (1) is saying that z is an odd integer. So, any base raised to z will keep its sign (i.e., whether the expression is positive or negative will not change since the base is raised to an odd exponent).
      z/2 = not integer if z is odd
      z/2 = integer if z is even
    2. Remember that (nk)z = (nz)(kz). So, Statement (1) says that (nz)(kz) > 0. It is important to know that there are two ways that a product of two numbers can be greater than zero:
      Case 1: (negative number)(negative number) > 0
      Case 2: (positive number)(positive number) > 0
    3. Since you know that n < 0, we are dealing with Case 1 and Statement (1) can be simplified even further:
      (negative number)(k(odd exponent)) > 0.
    4. Since k will not change its sign when raised to an odd exponent, the equation can be simplified even further:
      (negative number)(k) > 0. k must be a negative number. Otherwise, this inequality will not be true.
    5. To summarize in algebra:
      (nk)z > 0
      (nk)z = (nz)(kz)
      (nz)(kz) > 0
      (negative number)(negative number) > 0
      or (positive number)(positive number) > 0
      (negative number)(k(odd exponent)) > 0
      (negative number)(k) > 0
      k is negative
    6. Since k is a negative number, k37 < 0. Statement (1) is SUFFICIENT.
  6. Evaluate Statement (2) alone.
    1. Statement (2) says that k is less than n. Since you know that n is less than 0, Statement (2) says that k is less than a negative number. Only a negative number is less than another negative number. So, k must also be a negative number. Consequently, k37 will always be less than 0 since (negative)odd < 0. Statement (2) is SUFFICIENT.
    2. Summarizing in algebra:
      k < n < 0
  7. Since Statement (1) alone is SUFFICIENT and Statement (2) alone is SUFFICIENT, answer D is correct.
GMAT Classic Mock Test - 6 - Question 27
Save

What is the area of isosceles triangle X?

  1. The length of the side opposite the single largest angle in the triangle is 6cm
  2. The perimeter of triangle X is 16cm
Detailed Solution for GMAT Classic Mock Test - 6 - Question 27
  1. In a triangle, the side opposite the largest angle will be the longest. Correspondingly, the side opposite the smallest angle will be the shortest.
  2. Evaluate Statement (1) alone.
    1. The side opposite the single largest angle must be the single largest side in the triangle. Since an isosceles triangle contains two equal sides and two equal angles yet we know that a "single largest angle" exists, the side opposite the single largest angle cannot be one of these equal sides. If the longest side of an isosceles triangle were one of its equal sides, both angles opposite the equal sides would have equal measurement and there would be no single largest angle as Statement (1) indicates there must be.
    2. The single largest side must be the base since the two other angles will have equivalent measurements and thus the length of the sides opposite them will be equivalent. The two equal sides must be less than 6cm (otherwise, the angle opposite the base would not be the single largest angle in the triangle). To reiterate, the two angles opposite the equivalent sides must be smaller than the angle opposite the base (otherwise the angle opposite 6cm side would not be the single largest angle).
    3. The two equal sides must be longer than 3cm. Otherwise a closed triangle could not be formed (i.e., the lines would not connect).
    4. Draw a diagram with the information we know:


      AC = 6
      3cm < AB < 6cm
      3cm < BC < 6cm
    5. Although we know the base, we know nothing about the height, BD. Without knowing that a definitive value for the height exists, we cannot calculate the area of the triangle.
    6. Statement (1) is NOT SUFFICIENT.
  3. Evaluate Statement (2) alone.
    1. Since triangle X is an isosceles triangle, the perimeter is formed by adding two equal sides and a third side. Set up an equation to reflect this:
      2L + N = 16 where L is the length of the equivalent sides of the triangle and N is the length of the other side.
    2. There are many different combinations of L and N that would give a different area. Assume that N is the base:
      If N = 4 and L = 6, then the height of the triangle (via the Pythagorean theorem) would be the square root of 32, which is 5.65
      If N = 5 and L = 5.5, then the height of the triangle (via the Pythagorean theorem) would be the square root of 24, which is 4.89.
    3. Without being able to determine that a definitive value for the base and height exists, we cannot calculate the area of the triangle.
    4. Statement (2) is NOT SUFFICIENT.
  4. Evaluate Statements (1) and (2) together.
    1. Write equations that are derived from the information in both Statements:
      (1) Base = 6cm
      (2) 2L + B = 16
    2. Combine the two equations:
      2L + 6 = 16
      L = 5
    3. We now have a right triangle formed by half the base (AD = 3), the height (BD = unknown), and an equal side (AB = 5).


      AC = 6
      AD = 3
      AB = BC = 5
      Note: Since the triangle is isosceles, the height (or line BD) must perfectly bisect the base. This is because angles A and C are equal and sides AB and BC are equal. Further, angle D is right since it is the height and the height is by definition a right angle.
    4. Through the Pythagorean theorem, BD must equal 4:
      (AD)2 + (BD)2 = (AB)2
      9 + (BD)2 = 25
      (BD)2 = 16
      BD = 4
    5. The area of triangle X must be (1/2)Base x Height = 3(4) = 12
    6. Statements (1) and (2), when taken together, are SUFFICIENT.
  5. Since Statement (1) alone is NOT SUFFICIENT and Statement (2) alone is NOT SUFFICIENT, but Statements (1) and (2), when taken together are SUFFICIENT, answer C is correct.
GMAT Classic Mock Test - 6 - Question 28
Save

For a set of 3 numbers, assuming there is only one mode, does the mode equal the range?

  1. The median equals the range
  2. The largest number is twice the value of the smallest number
Detailed Solution for GMAT Classic Mock Test - 6 - Question 28
  1. The mode is the number that appears the most times in the set, and the median is the middle number when the set is sorted from least to greatest. The range is the largest value in the set minus the smallest value.
  2. Given that there is only one mode, at least two of the numbers must be equal. In particular, either all the numbers are equal, or two of the numbers are equal and the third is different.
  3. Evaluate Statement (1) alone.
    1. First, assume that all three of the numbers in the set are equal. Represent this set by {A, A, A}. The range is equal to A - A = 0, because the highest number and the lowest number in the set are the same.
    2. By Statement (1), the range is equal to the median. Since the range is 0, the median is 0. Now the set can be represented by {A, 0, A}, since the median is the middle number. But all the numbers in the set are the same, so A = 0 and the set can be represented by {0, 0, 0}. The mode is 0 because this is the number that appears the most times.
    3. Therefore, when all three numbers in the set are equal, the mode is equal to the range.
    4. Now, assume that only two of the numbers in the set are equal. The set can be represented as {A, A, B}, where A is not the same as B. When sorted from least to greatest, the set become either {A, A, B} or {B, A, A}. The median of both of these sets is A. By Statement (1), the range is A because the range is equal to the median. The mode is also A, because it appears in the set more times than B.
    5. Therefore, when only two numbers in the set are equal, the mode is equal to the range.
    6. Whether three numbers in the set are equal, or only two, the mode is always equal to the range.
    7. Statement (1) is SUFFICIENT.
  4. Evaluate Statement (2) alone.
    1. First, assume that all three of the numbers in the set are equal. Represent this set by {A, A, A}. Statement (2) says that A = 2A, because A is both the largest number and the smallest number in the set. The only way A = 2A is if A = 0.
    2. When A = 0, the set becomes {0, 0, 0}. The range is 0 - 0 = 0, and the mode is 0. Thus, the mode equals the range when all three numbers are equal.
    3. Now, assume that only two of the numbers in the set are equal. The set can be represented as {A, A, B}, where A is not the same as B. When sorted from least to greatest, the set become either {A, A, B} or {B, A, A}. Statement (2) says that A = 2B, or B = 2A, depending on whether A or B is larger.
    4. Assuming A is the larger number, A = 2B. For example, A = 8 and B = 4. Then the sorted set becomes {4, 8, 8}. In this case, the range is 8 - 4 = 4. The mode is 8, because it appears the most times in the set. The mode is NOT equal to the range.
    5. Now, assume B is the larger number, B = 2A. For example, A = 3 and B = 6. Then the sorted set becomes {3, 3, 6}. In this case, the range is 6 - 3 = 3. The mode is 3. The mode is equal to the range in this case.
    6. Whether or not the mode is equal to the range depends on whether A or B is larger. Therefore the answer cannot be determined from Statement (2) alone.
    7. Statement (2) is NOT SUFFICIENT.
  5. Since Statement (1) alone is SUFFICIENT and Statement (2) alone is NOT SUFFICIENT, answer A is correct.
GMAT Classic Mock Test - 6 - Question 29
Save

Q is less than 10. Is Q a prime number?

  1. Q2 - 2 = P; P is prime and P < 10.
  2. Q + 2 is NOT prime, but Q is a positive integer.
Detailed Solution for GMAT Classic Mock Test - 6 - Question 29
  1. Evaluate Statement (1) alone.
    1. First solve the equation from Statement (1) for P.
      Q2 - 2 = P
      Q2 = P + 2
      Q = Sqrt(P + 2)
    2. Since P is a prime less than 10, try the possible values for
    3. As seen in the table, when P = 2 or P = 7, then Q is prime. Otherwise, Q is not a prime number, nor even an integer. Whether Q is prime or not depends on P, so the question cannot be answered.
    4. Statement (1) is NOT SUFFICIENT.
  2. Evaluate Statement (2) alone.
    1. Since Q + 2 is not prime, let L be a number that is not prime, and L = Q + 2. Examine two different examples for L.
    2. Let L = 4. This implies that Q = 2, which is a prime number.
    3. Let L = 8. This implies that Q = 6, which is not a prime number.
    4. Whether Q is prime or not depends on L, so the question cannot be answered.
    5. Statement (2) is NOT SUFFICIENT.
  3. Evaluate Statement (1) and (2) together.
    1. From the table above, only two values of P allow for Q to be an integer--which is demanded in Statement (2). In particular, when P = 2, Q = 2 and when P = 7, Q = 3.
    2. So far, there are only two possibilities for values of Q. Now apply Statement (2). Q + 2 may not be a prime number. Thus, the case where Q = 3 is no longer a possibility because Q + 2 = 5, which is a prime number.
    3. The only possibility that remains after applying Statements (1) and (2) is Q = 2. Thus, Q is a prime number.
    4. Statement (1) and (2) together are SUFFICIENT.
  4. Since Statement (1) alone is NOT SUFFICIENT and Statement (2) alone is NOT SUFFICIENT yet Statements (1) and (2), when taken together, are SUFFICIENT, answer C is correct.
GMAT Classic Mock Test - 6 - Question 30
Save

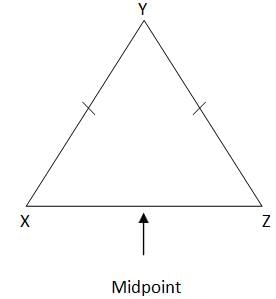
X, Y, and Z are three points in space; is Y the midpoint of XZ?

  1. ZY and YX have the same length
  2. XZ is the diameter of a circle with center Y
Detailed Solution for GMAT Classic Mock Test - 6 - Question 30
  1. Evaluate Statement (1) alone.
    1. It is possible that XZ is a straight line with Y as the midpoint, making ZY=YX.
    2. However, just because ZY = YX does not mean Y must always be the midpoint; XYZ could be an equilateral triangle.

    3. Statement (1) alone is NOT SUFFICIENT.
  2. Evaluate Statement (2) alone.
    1. By definition, the center of a circle is the midpoint of a diameter. Consequently, XZ runs through point Y and XY = YZ since both are radii and all radii must be the same length.
    2. Statement (2) alone is SUFFICIENT.
  3. Since Statement (1) alone is NOT SUFFICIENT but Statement (2) alone is SUFFICIENT, answer B is correct.
View more questions
Information about GMAT Classic Mock Test - 6 Page
In this test you can find the Exam questions for GMAT Classic Mock Test - 6 solved & explained in the simplest way possible. Besides giving Questions and answers for GMAT Classic Mock Test - 6, EduRev gives you an ample number of Online tests for practice

Top Courses for GMAT

Download as PDF

Top Courses for GMAT

Important Questions for GMAT Classic Mock Test - 6

Find all the important questions for GMAT Classic Mock Test - 6 at EduRev.Get fully prepared for GMAT Classic Mock Test - 6 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the GMAT Classic Mock Test - 6 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of GMAT Classic Mock Test - 6 resources.

GMAT Classic Mock Test - 6 MCQs with Answers

Prepare for the GMAT Classic Mock Test - 6 within the GMAT exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for GMAT Classic Mock Test - 6

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace GMAT Classic Mock Test - 6 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup