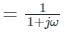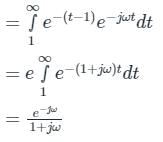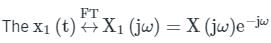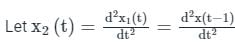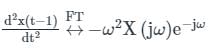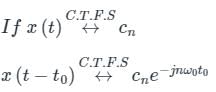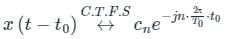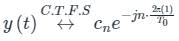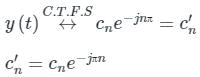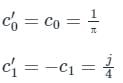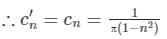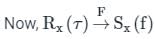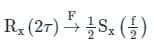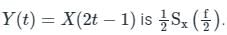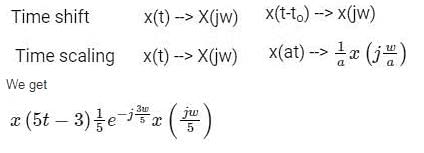Test: Time Shifting & Scaling Property - Electrical Engineering (EE) MCQ
10 Questions MCQ Test - Test: Time Shifting & Scaling Property
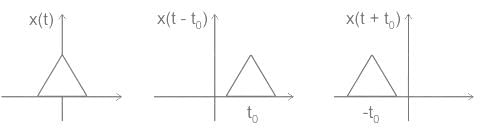
The given mathematical representation belongs to:
y(t) = x(t - T)
y(t) = x(t - T)
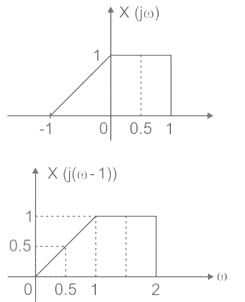
The Fourier transform of a signal x(t), denoted by X(jω), is shown in the figure.
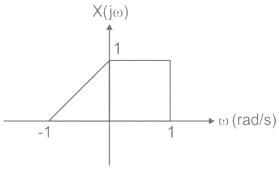
Let y(t) = x(t) + ejtx(t). The value of Fourier transforms of y(t) evaluated at the angular frequency ω = 0.5 rad/s is

Let y(t) = x(t) + ejtx(t). The value of Fourier transforms of y(t) evaluated at the angular frequency ω = 0.5 rad/s is
For a signal x(t) = e-t+1 u(t-1) Fourier transform is
A real valued signal x(t) limited to frequency band |f| < ω/2 is passed through an LTI system whose frequency response is
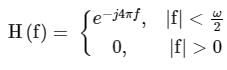
The output of the system is
The Fourier transform of x(t) is X(jω). Then, the Fourier transform of 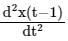
Let x(t) and y(t) (with Fourier transform X(ω) and Y(ω) be related as shown in figure below
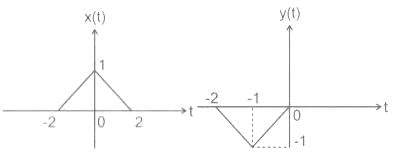
Then Y(ω) in terms of X(ω) is
The Fourier series coefficients of signal x(t) shown in Figure (A) are given as:
c0 = 1/π, c1 = −j/4, cn = 1/π(1 − n2), for k even.
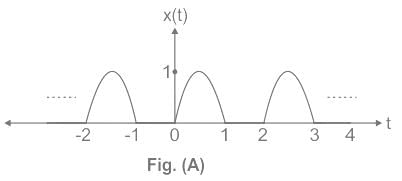
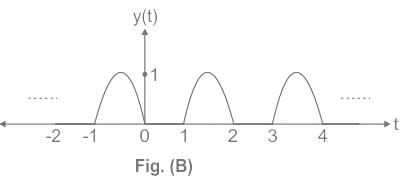
Which of the following Fourier series coefficients of y(t) shown in Figure (B) is/are correct?
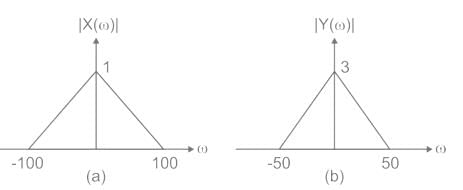
The magnitude of Fourier transform X(ω) of a function x(t) is shown below in figure (a). The magnitude of Fourier transform Y(ω) of another function y(t) is shown in figure (b). The phases of X(ω) and Y(ω) are zero for all ω. The magnitude and frequency units are identical in both the figures. The function y(t) can expressed in terms of x(t) as
Let X(t) be Wide Sense Stationary random process with power spectral density Sx(f). If Y(t) is a random process defined as Y(t) = X(2t − 1), the power spectral density Sy(f) is:
Let x(t)<-> X(jω) be Fourier Transform pair. The Fourier Transform of the signal x(5t-3) in terms of X(jω) is given as