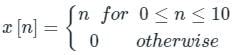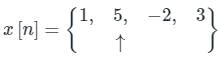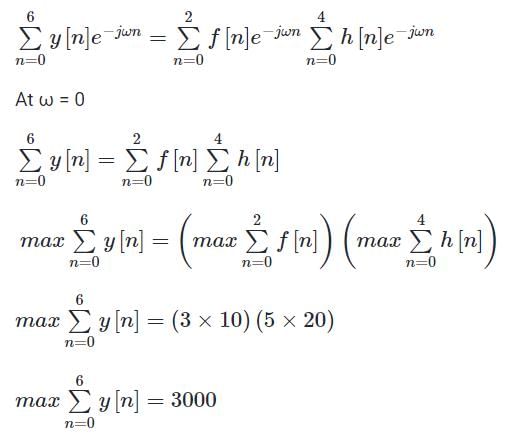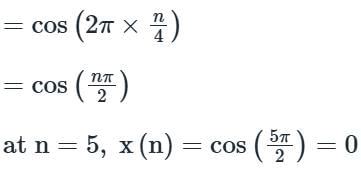Test: Discrete Time Signals - Electrical Engineering (EE) MCQ
15 Questions MCQ Test - Test: Discrete Time Signals
Which of the following is NOT one of the representations of discrete-time signals?
Which type/s of discrete-time system do/does not exhibit the necessity of any feedback?
The discrete-time system y(n) is the resultant convolution of f(n) and h(n) having lengths 3 and 5 respectively. The maximum possible sample value of f(n) and h(n) are 10 and 20 respectively. Find the maximum possible value of sum of all sample value of y(n).
Express the following finite discrete-time signal as the difference of two unit step sequences: x[n] = 1, for 0 ≤ n ≤ 5; and 0 otherwise.
The discrete time system described by y(n) = [x(n)]2 is
The special case of a finite-duration sequence is given as
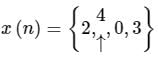
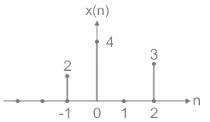
The sequence x(n) into a sum of weighted impulse sequences will be
What is the nature of the following function: y[n] = y[n-1] + x[n]?
Determine the product of two signals: x1 (n) = {2, 1, 1.5, 3}; x2 (n) = { 1, 1.5, 0, 2}.
Determine the discrete-time signal: x(n) = 1 for n ≥ 0 and x(n) = 0 for n < 0
Determine the value of the summation: ∑∞n= -∞ δ(n + 3)(n2 + n).
Unit Impulse function is obtained by using the limiting process on which among the following functions?
If the discrete time signals x1(n) = {2, 2, 1, 2} and x2(n) = { -2, -1, 3, 2}, then x1(n) + x2(n) = ?
If a continuous-time signal x(t) = cos(2πt) is sampled at 4 Hz, the value of the discrete-time sequence x(n) at n = 5 is