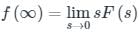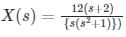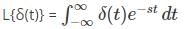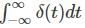Test: Laplace Analysis of Networks - Electrical Engineering (EE) MCQ
15 Questions MCQ Test - Test: Laplace Analysis of Networks
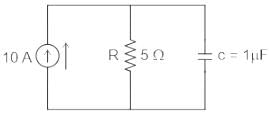
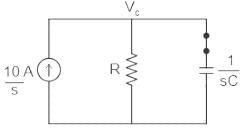
For the RC parallel circuit, determine the voltage across the capacitor using Laplace transform, assume capacitor is initially relaxed.

Calculate the transfer function of a system if the response is c(t) = e-6t for t > 0.
Given the input signal is an impulse signal.
What will be the transfer function of the system shown below?
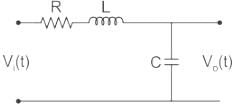

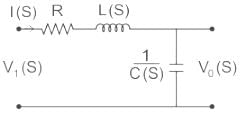
The voltage transfer function of the network shown in the figure below is
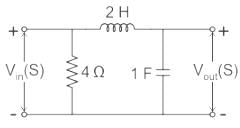
Which of the following is NOT one of the properties of transfer function?
If the step response to the input step amplitude of 1 V is given by Vo(t) = (1 - e-t / RC), the network can be represented by:
The transfer function of a linear system is the
The average power consumed by the following circuit is
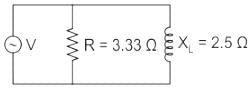
Vrms = 20∠ 53.13°V
Any system is said to be stable if and only if ____________
The transfer function of a system having the input as X(s) and output as Y(s) is?


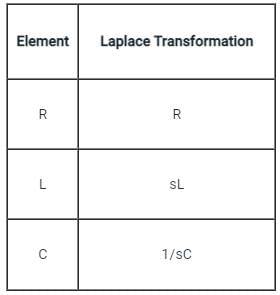
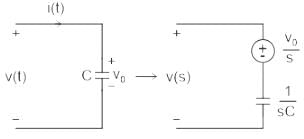
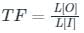
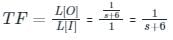



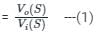
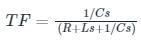
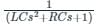
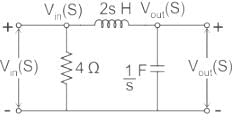
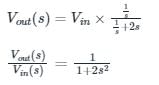

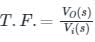
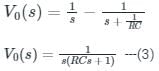

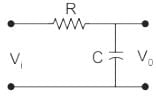
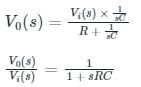
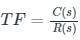
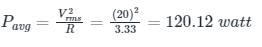
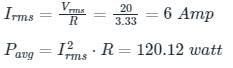
 will be
will be