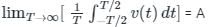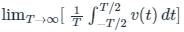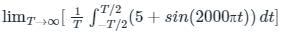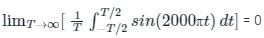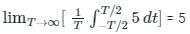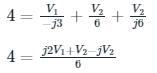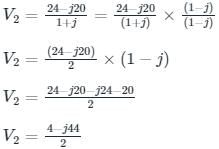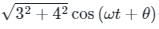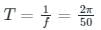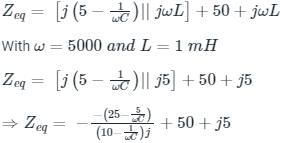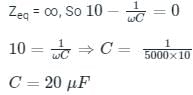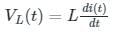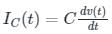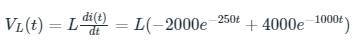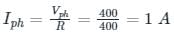Test: KCL & KVL in AC Circuits - 1 - Electrical Engineering (EE) MCQ
10 Questions MCQ Test - Test: KCL & KVL in AC Circuits - 1
An AC voltage is given by v(t) = 5 + sin(2000πt), what is the time period and the dc component in v(t)?
If the voltage and current in an A.C. circuit is 90° out of phase, then the power in the circuit will be -
In the case of a sinusoidal current, the unit of the amplitude is:
A sinusoid wave is expressed as 5 sin(4πt – 60°). Find the frequency.
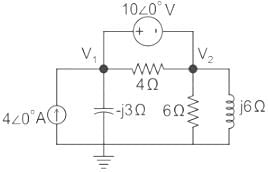
In the circuit shown in the figure, the value of node voltage ��2 is

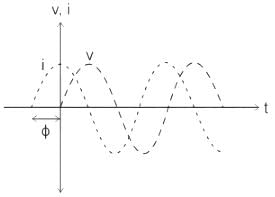
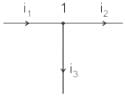
Three currents i1, i2 and i3 meet at a node as shown in the figure. If i1 = 3 cos (ωt) ampere, i2 = 4 sin (ωt) ampere and i3 = I3 cos (ωt + θ) ampere, the value of I3 in ampere is
What will be the period of the sinusoid, v(t) = 12 cos (50t + 30°)?
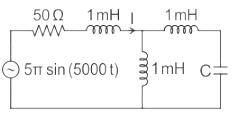
In the circuit shown, the current I flowing through the 50 Ω resistor will be zero if the value of capacitor C (in μF) is ______.
Consider a current source i(t) connected across a 0.5 mH inductor, where i(t) = 0 A for t < 0 and i(t) = (8e-250t - 4e-1000t) A for t ≥ 0. The voltage across the inductor at t = 0 s is
Three 400 Ω resistors are connected in delta and powered by a 400 V (rms), 50 Hz balanced, symmetrical R - Y - B sequence, three-phase three-wire mains. The rms value of the line current (in amperes, rounded off to one decimal place) is