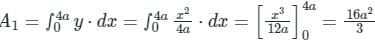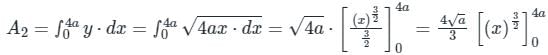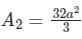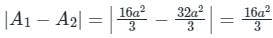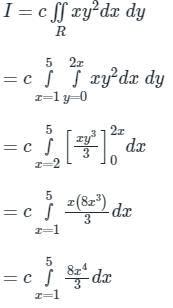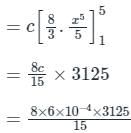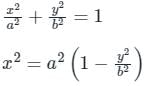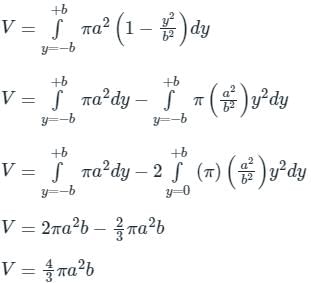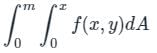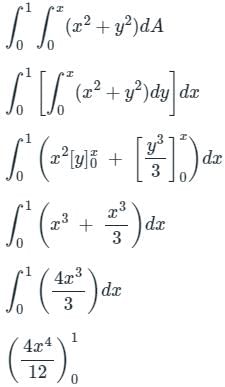Test: Multiple Integrals - Engineering Mathematics MCQ
15 Questions MCQ Test - Test: Multiple Integrals
The following surface integral is to be evaluated over a sphere for the given steady vector field, F = xi + yj + zk defined with respect to a Cartesian coordinate system having i, j, and k as unit base vectors.
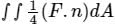 , Where S is the sphere, x2 + y2 + z2 = 1 and n is the outward unit normal vector to the sphere. The value of the surface integral is
, Where S is the sphere, x2 + y2 + z2 = 1 and n is the outward unit normal vector to the sphere. The value of the surface integral is
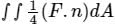 , Where S is the sphere, x2 + y2 + z2 = 1 and n is the outward unit normal vector to the sphere. The value of the surface integral is
, Where S is the sphere, x2 + y2 + z2 = 1 and n is the outward unit normal vector to the sphere. The value of the surface integral isThe value of the integral 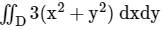 , where D is the shaded triangular region shown in the diagram, is _____ (rounded off to the nearest integer).
, where D is the shaded triangular region shown in the diagram, is _____ (rounded off to the nearest integer).
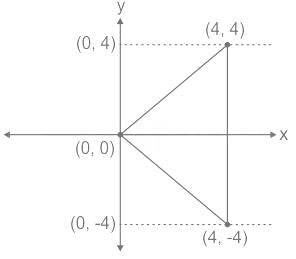
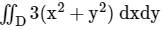 , where D is the shaded triangular region shown in the diagram, is _____ (rounded off to the nearest integer).
, where D is the shaded triangular region shown in the diagram, is _____ (rounded off to the nearest integer).
A definite double integral is given below, then, evaluation of the double integral over the region R will be __
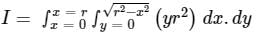
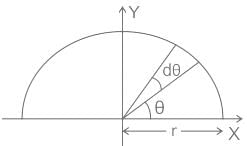
Where R is the region on X - Y plane for the function given as, 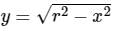 and r ∈ [0, 5]
and r ∈ [0, 5]
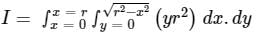
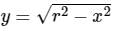 and r ∈ [0, 5]
and r ∈ [0, 5] The integral 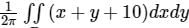 , where D denotes the disc ��2 + ��2 ≤ 4, evaluates to__________.
, where D denotes the disc ��2 + ��2 ≤ 4, evaluates to__________.
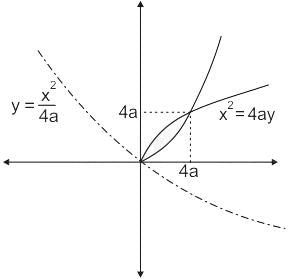
The area bounded by the curves y2 = 9x, x – y + 2 = 0 is given by
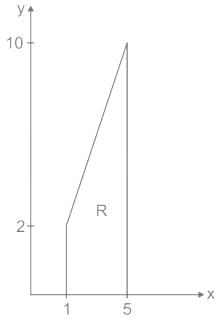
Let 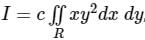 , where R is the region shown in the figure and c = 6 × 10-4. The value of I equals________. (Give the answer up to two decimal places.)
, where R is the region shown in the figure and c = 6 × 10-4. The value of I equals________. (Give the answer up to two decimal places.)
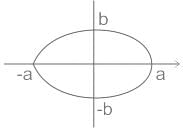
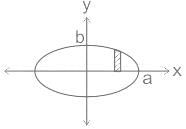
An ellipse 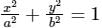 is revolved around the y-axis. The volume generated by the solid of revolution if a = 3 and b = 2 is______
is revolved around the y-axis. The volume generated by the solid of revolution if a = 3 and b = 2 is______
The value of 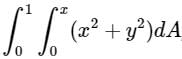 , where dA indicate small area in xy - plane, is
, where dA indicate small area in xy - plane, is


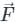 taken over a closed surface ‘S’ is equal to the volume integral of the divergence of that vector function
taken over a closed surface ‘S’ is equal to the volume integral of the divergence of that vector function  taken over a volume enclosed by the closed surface ‘S’.
taken over a volume enclosed by the closed surface ‘S’.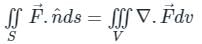
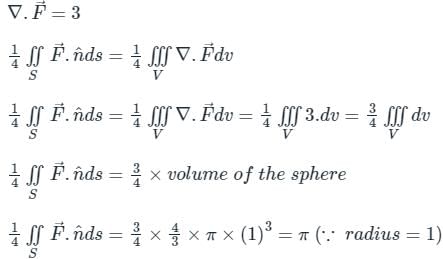
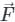 around any closed surface C is equal to the surface integral of the normal component of the curl of vector
around any closed surface C is equal to the surface integral of the normal component of the curl of vector 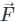 over an unclosed surface ‘S’.
over an unclosed surface ‘S’.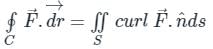
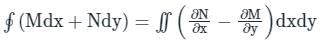
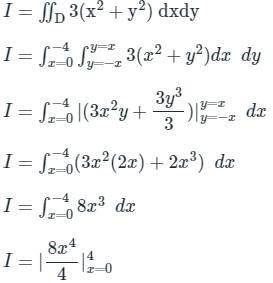

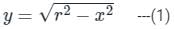
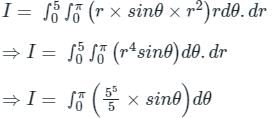
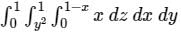
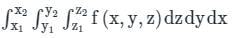
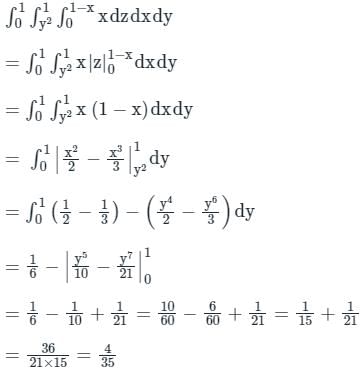
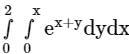 is
is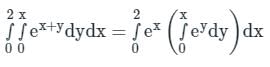
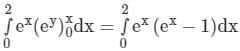
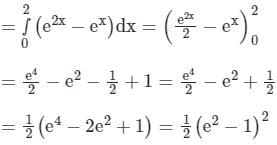
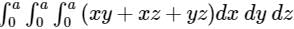 .
.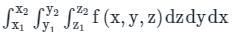
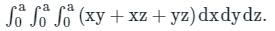
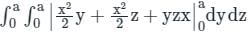
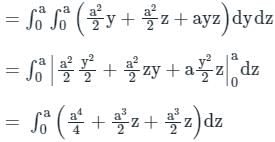
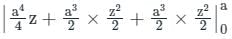
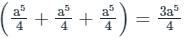
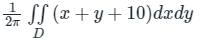
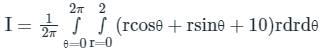
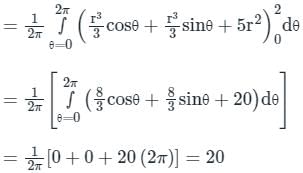
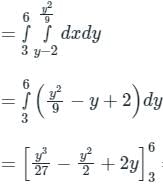
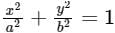 is
is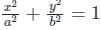
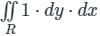
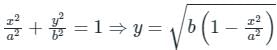
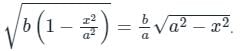
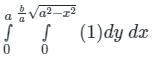
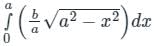
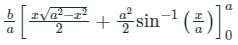
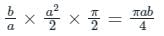
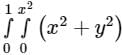 equals to
equals to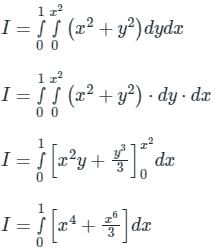
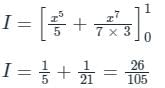
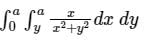
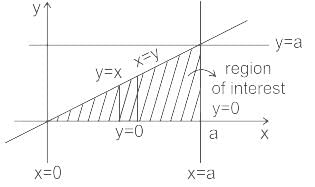
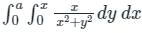 is the correct solution.
is the correct solution.