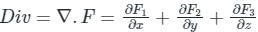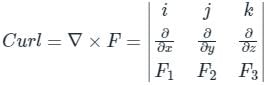Test: Stokes Theorem - Engineering Mathematics MCQ
15 Questions MCQ Test - Test: Stokes Theorem
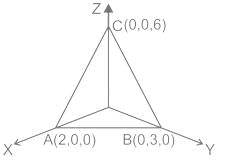
By applying Stokes theorem, the value of 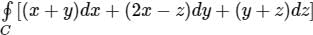 where C is the boundary of the triangle with vertices (2, 0, 0), (0, 3, 0) and (0, 0, 6), is
where C is the boundary of the triangle with vertices (2, 0, 0), (0, 3, 0) and (0, 0, 6), is
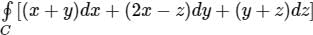 where C is the boundary of the triangle with vertices (2, 0, 0), (0, 3, 0) and (0, 0, 6), is
where C is the boundary of the triangle with vertices (2, 0, 0), (0, 3, 0) and (0, 0, 6), isConsider a vector field 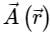 . The closed loop line integral
. The closed loop line integral 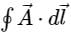 can be expressed as
can be expressed as
Stokes' theorem is valid irrespective of
1. Shape of closed curve C
2. Type of vector A
3. Type of coordinate system
4. Whether the surface is closed or open
Which of the above statements are correct?
Which of the following theorem convert line integral to surface integral?
The Stoke’s theorem can be used to find which of the following?
The conductivity of a material with current density 1 unit and electric field 200 μV is
The voltage of a capacitor 12F with a rating of 2J energy is
Find the value of Stoke’s theorem for A = x i + y j + z k. The state of the function will be
Stoke's theorem is primarily concerned with the relationship between:


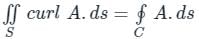
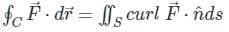
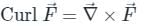
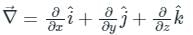





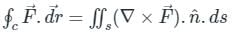
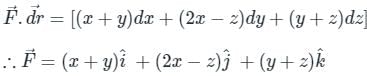
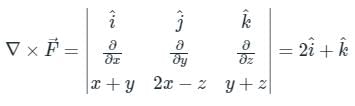
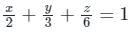




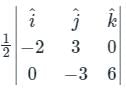
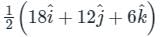

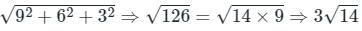
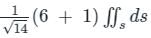
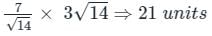
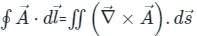
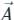 around a (closed) path L is equal to the surface integral of the curl of
around a (closed) path L is equal to the surface integral of the curl of 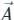 over the open surface, S bounded by L (fig).
over the open surface, S bounded by L (fig).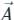 and
and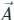 are continuous on S.
are continuous on S.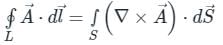
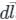 and
and 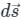 involved in Stokes’s theorem
involved in Stokes’s theorem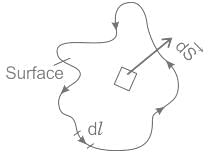
 is an axial (or rotational) vector whose magnitude is the maximum circulation of
is an axial (or rotational) vector whose magnitude is the maximum circulation of 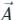 per unit area as the area tends to zero and whose direction is the normal direction of the area is oriented to make the circulation maximum.
per unit area as the area tends to zero and whose direction is the normal direction of the area is oriented to make the circulation maximum.