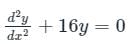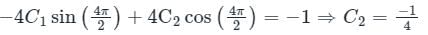Test: Higher Order Linear Differential Equations with Constant Coefficients - 1 - Mechanical Engineering MCQ
10 Questions MCQ Test - Test: Higher Order Linear Differential Equations with Constant Coefficients - 1
A simple mass-spring oscillatory system consists of a mass m, suspended from a spring of stiffness k. Considering z as the displacement of the system at any time t, the equation of motion for the free vibration of the system is 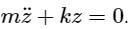 The natural frequency of the system is
The natural frequency of the system is
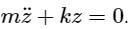 The natural frequency of the system is
The natural frequency of the system isThe solution of the differential equation, for t > 0, y″(t) + 2y′(t) + y(t) = 0 with initial conditions y′(0) = 1and y(0) = 0, is u(t) denotes the unit step functions).
The solution to the differential equation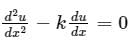 where k is a constant, subjected to the boundary conditions u(0) = 0 and u(L) = U, is
where k is a constant, subjected to the boundary conditions u(0) = 0 and u(L) = U, is
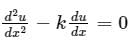 where k is a constant, subjected to the boundary conditions u(0) = 0 and u(L) = U, is
where k is a constant, subjected to the boundary conditions u(0) = 0 and u(L) = U, isA function y(t) such that y(0) = 1 and y(1) = 3e-1, is a solution of the differential equation 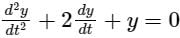 . Then y(2) is
. Then y(2) is
Consider the following statements about the linear dependence of the real valued functions y1 = 1, y2 = x and y3 = x2, over the field of real numbers.
I. y1, y2 and y3 are linearly independent on – 1 ≤ x ≤ 0
II. y1, y2 and y3 are linearly dependent on 0 ≤ x ≤ 1
III. y1, y2 and y3 are linearly independent on 0 ≤ x ≤ 1
IV. y1, y2 and y3 are linearly dependent on – 1 ≤ x ≤ 0
Which one among the following is correct?
For the Ordinary Differential Equation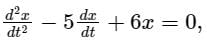 with initial conditions x(0) = 0 and dx/dt(0) = 10, the solution is
with initial conditions x(0) = 0 and dx/dt(0) = 10, the solution is
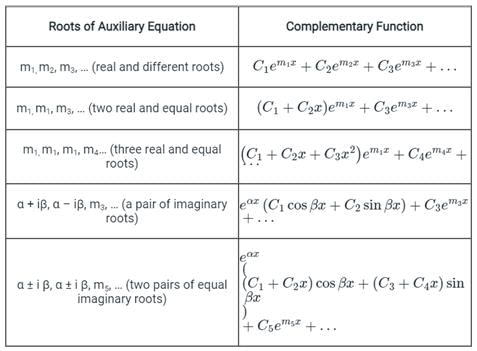
If roots of the auxiliary equation of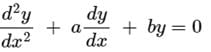 are real and equal, the general solution of the differential equation is
are real and equal, the general solution of the differential equation is
The general solution of the differential equation  in terms of arbitrary constants K1 and K2 is:
in terms of arbitrary constants K1 and K2 is:
The complete solution of the linear differential equation
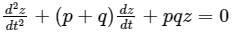
The differential equation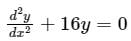 For y(x) with the two boundary conditions
For y(x) with the two boundary conditions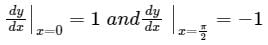



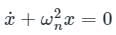 (Standard Differential Equation for Spring)
(Standard Differential Equation for Spring)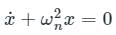
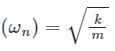


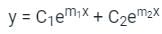
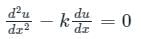
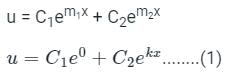
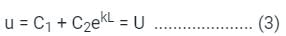
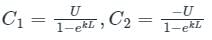
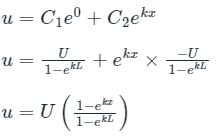

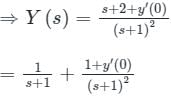
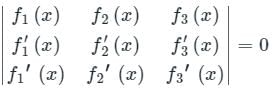
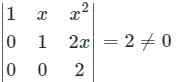
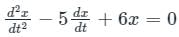
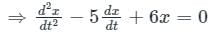
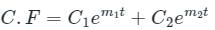
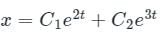
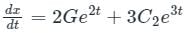
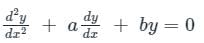
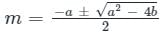
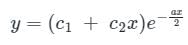
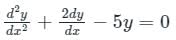
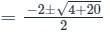
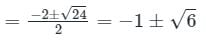
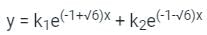

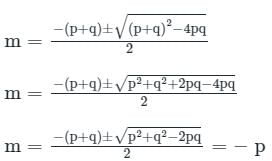
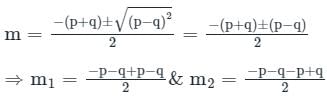
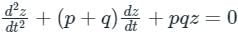 is c1 e-pt + c2 e-qt
is c1 e-pt + c2 e-qt