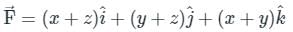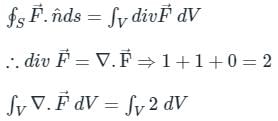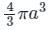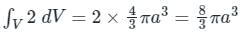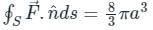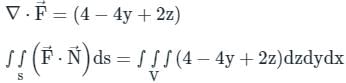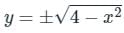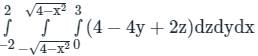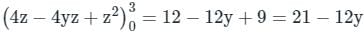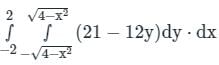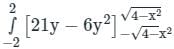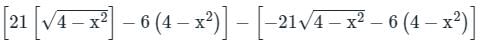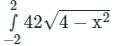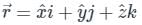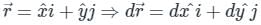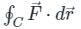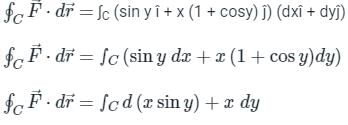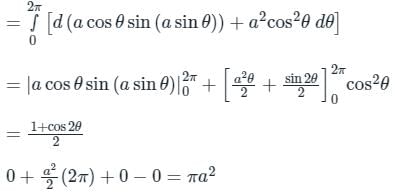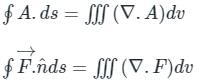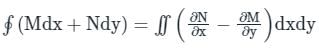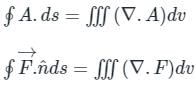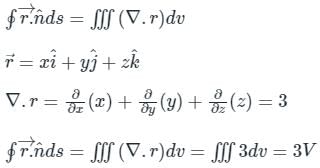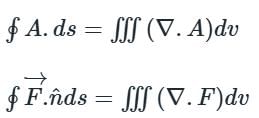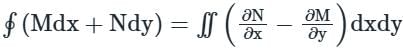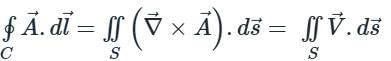Test: Gauss's Theorem - Engineering Mathematics MCQ
15 Questions MCQ Test - Test: Gauss's Theorem
Consider a cube of unit edge length and sides parallel to co-ordinate axes, with its centroid at the point (1, 2, 3). The surface integral 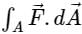 of a vector field
of a vector field  over the entire surface A of the cube is ______.
over the entire surface A of the cube is ______.
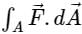 of a vector field
of a vector field  over the entire surface A of the cube is ______.
over the entire surface A of the cube is ______.If C is the plane triangle which is enclosed by the lines x = π/2,y = 2/πx and y = 0, then the value of following integral ∫C[cosxdy + (y − sinx)dx] comes out to be π/a + b/π. Find |ab|
The value of ∫S(x + z)dydz + (y + z)dxdz + (x + y)dxdy, Where ‘S’ is the surface of the sphere x2 + y2 + z2 = 4, is ___
If 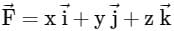 and s is the closed surface of x2 + y2 + z2 = a2. Then
and s is the closed surface of x2 + y2 + z2 = a2. Then  is
is
If S is the surface of the sphere x2 + y2 + z2 = a2, then the value of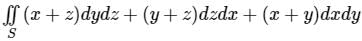 is
is
By Gauss divergence theorem the value of 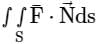 where
where 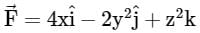 and S is x2 + y2 = 4, z = 0, z = 3 is
and S is x2 + y2 = 4, z = 0, z = 3 is
Evaluate the line integral of vector field F = sin y î + x (1 + cos y) ĵ along the circular path given by x2 + y2 = a2, z = 0 (Use a = 5 and round-off to two decimals)
Evaluate the surface integral ∫∫ (3x i + 2y j). dS, where S is the sphere given by x2 + y2 + z2 = 9.
A thin, metallic spherical shell contains a charge Q on it. A point charge q is placed at the centre of the shell and another charge q1 is placed outside it as shown in the following figure . All the three charges are positive. The force on the central charge due to the shell is
A charge Q is uniformly distributed over a large plastic plate. The electric field at a point P close to the centre of the plate is 10 V m−1. If the plastic plate is replaced by a copper plate of the same geometrical dimensions and carrying the same charge Q, the electric field at the point P will become
The value of the integral 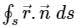 over the closed surface S bounding a volume V, where
over the closed surface S bounding a volume V, where 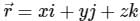 is the position vector and n̂ is normal to the surface S, is
is the position vector and n̂ is normal to the surface S, is


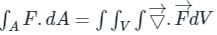
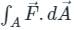 is called surface integral
is called surface integral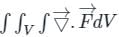 is called volume integral
is called volume integral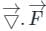 is called divergence of F
is called divergence of F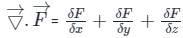
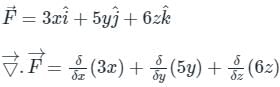

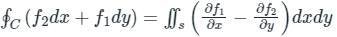
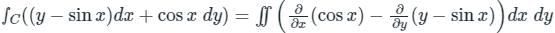


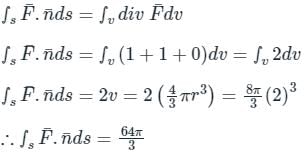
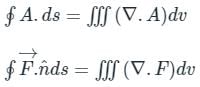
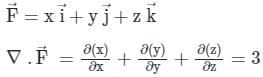
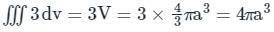
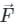 taken around a closed surface S is equal to the integral of the divergence of
taken around a closed surface S is equal to the integral of the divergence of  taken over the volume V enclosed by the surface S. Mathematically;
taken over the volume V enclosed by the surface S. Mathematically;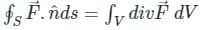
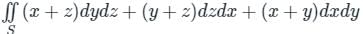 and x2 + y2 + z2 = a2
and x2 + y2 + z2 = a2