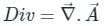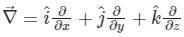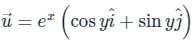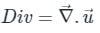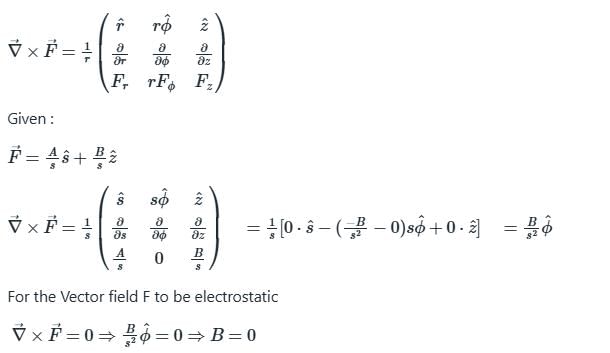Test: Divergence Theorem - Engineering Mathematics MCQ
15 Questions MCQ Test - Test: Divergence Theorem
Given a function ϕ = 1/2(x2 + y2 + z2) in three-dimensional Cartesian space, the value of the surface integral ∯S n̂ . ∇ϕ dS where S is the surface of a sphere of unit radius and n̂ is the outward unit normal vector on S, is
The value of 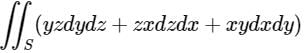 where S is the surface of unit sphere x2 + y2 + z2 = 1 is
where S is the surface of unit sphere x2 + y2 + z2 = 1 is
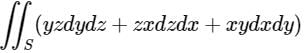 where S is the surface of unit sphere x2 + y2 + z2 = 1 is
where S is the surface of unit sphere x2 + y2 + z2 = 1 isConsider a closed surface S surrounding volume V. If 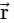 is the position vector of a point inside S, with the unit normal
is the position vector of a point inside S, with the unit normal 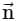 on S, the value of the integral
on S, the value of the integral 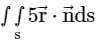 is
is
Find the value of 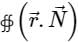 ds where
ds where 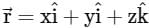 and S is the surface of sphere x2 + y2 + z2 = 16 ____
and S is the surface of sphere x2 + y2 + z2 = 16 ____
The divergence theorem for a surface consisting of a sphere is computed in which coordinate system?
The divergence theorem value for the function x2 + y2 + z2 at a distance of one unit from the origin is
Find the divergence theorem value for the function given by (ez, sin x, y2)
The value of the surface integral 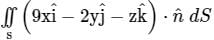 over the surface S of the sphere x2 + y2 + z2 = 9, where n is the unit outward normal to the surface element dS, is _______.
over the surface S of the sphere x2 + y2 + z2 = 9, where n is the unit outward normal to the surface element dS, is _______.
The value of ∯ (4xî - 2y2j + z2k).n̂ds where S is bounded by x2 + y2 = 4, Z = 0 and Z = 3 is
Identify the nature of the field, if the divergence is zero and curl is also zero.
Find whether the vector is solenoidal, E = yz i + xz j + xy k
A vector field is expressed in the cylindrical coordinate system (s,Ô, z) as,
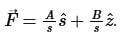
If this field represents an electrostatic field, then the possible values of A and B, respectively, are




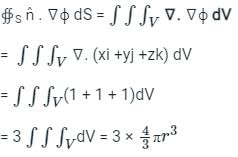
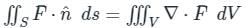
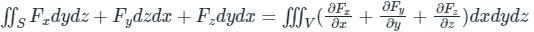
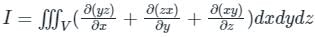
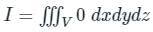

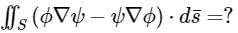
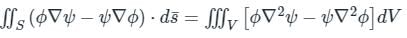
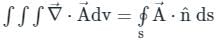
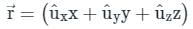
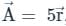 ,
, 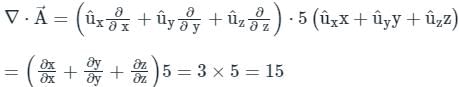
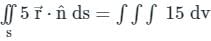
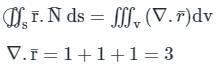
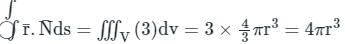
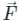 taken over a closed surface ‘S’ is equal to the volume integral of the divergence of that vector function
taken over a closed surface ‘S’ is equal to the volume integral of the divergence of that vector function 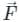 taken over a volume enclosed by the closed surface ‘S’.
taken over a volume enclosed by the closed surface ‘S’.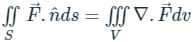

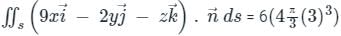
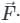 n̂ds = ∭ (∇ ⋅ F) dV
n̂ds = ∭ (∇ ⋅ F) dV 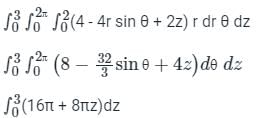
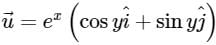
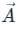 is defined as:
is defined as: