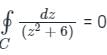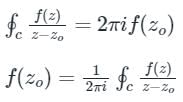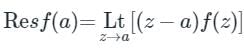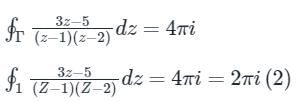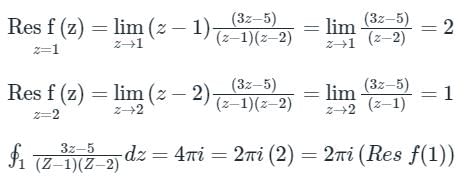Test: Cauchy’s Integral Theorem - 2 - Civil Engineering (CE) MCQ
10 Questions MCQ Test - Test: Cauchy’s Integral Theorem - 2
Let 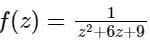 defined in the complex plane. The integral ∮c f(z)dz over the contour of a circle c with center at the origin and unit radius is ______.
defined in the complex plane. The integral ∮c f(z)dz over the contour of a circle c with center at the origin and unit radius is ______.
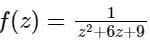 defined in the complex plane. The integral ∮c f(z)dz over the contour of a circle c with center at the origin and unit radius is ______.
defined in the complex plane. The integral ∮c f(z)dz over the contour of a circle c with center at the origin and unit radius is ______.Let f(z) = 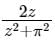 if C is a counter clock wise path in the z plane such that |z - i| = 2, then the value of
if C is a counter clock wise path in the z plane such that |z - i| = 2, then the value of 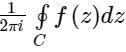 is____
is____
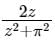 if C is a counter clock wise path in the z plane such that |z - i| = 2, then the value of
if C is a counter clock wise path in the z plane such that |z - i| = 2, then the value of 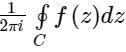 is____
is____The value of the integral
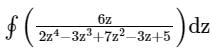
evaluated over a counter-clockwise circular contour in the complex plane enclosing only the pole z = i, where i is the imaginary unit, is
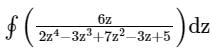
evaluated over a counter-clockwise circular contour in the complex plane enclosing only the pole z = i, where i is the imaginary unit, is
The quadratic approximation of (x) = x3 - 3x2 - 5 at the point x = 0 is
The closed loop line integral 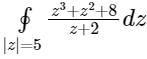 evaluated counter-clockwise, is
evaluated counter-clockwise, is
Given z = x +iy, i = √-1 C is a circle of radius 2 with the centre at the origin. If the contour C is traversed anticlockwise, then the value of the integral  is ________ (round off to one decimal place.)
is ________ (round off to one decimal place.)
Consider the integral
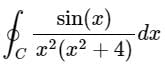
Where C is a counter-clockwise oriented circle defined as |x - i| = 2. The value of the integral is
C is a closed path in the z-plane given by |z| = 3. The value of the integral 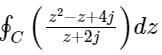 is
is
The value of 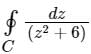 , where C is the boundary of |z - i| = 1, is
, where C is the boundary of |z - i| = 1, is
The value of 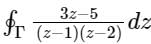 along a closed path Γ is equal to (4 π i), where z = x + iy and i = √-1. The correct path Γ is
along a closed path Γ is equal to (4 π i), where z = x + iy and i = √-1. The correct path Γ is


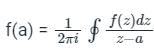
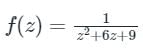
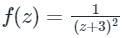

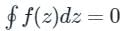
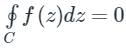

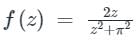
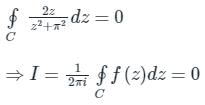

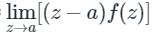
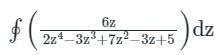
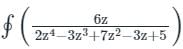 dz = 2πi (Residue at z = i )
dz = 2πi (Residue at z = i )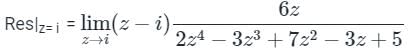
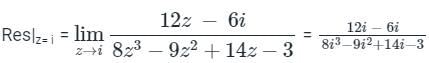
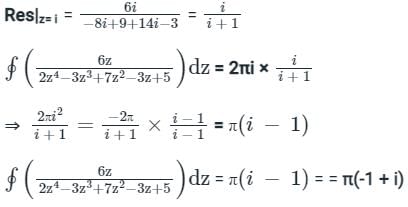
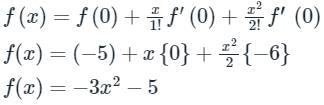
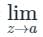 a[(z−α)f(z)]
a[(z−α)f(z)]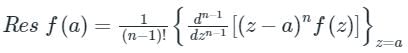
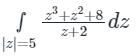
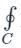 f(x) dz = 2πi × (sum of residues)
f(x) dz = 2πi × (sum of residues)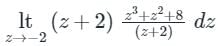
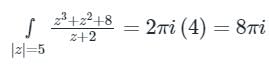
 f(Z)dz = 2πi × [sum of residues at singular points within C]
f(Z)dz = 2πi × [sum of residues at singular points within C]
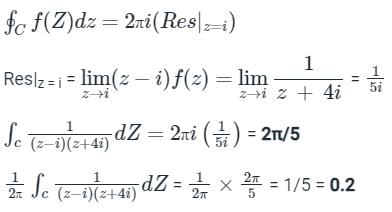
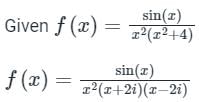
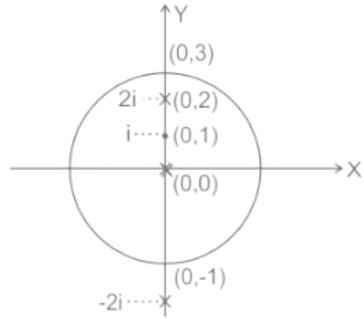

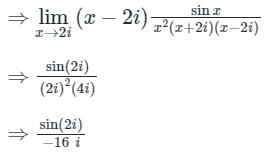
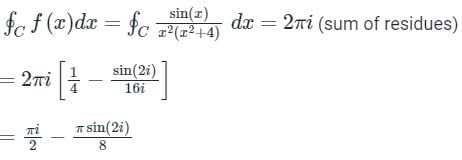
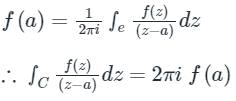
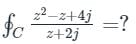
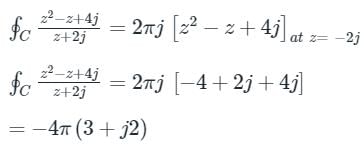
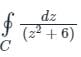 where C is |z -i| = 1
where C is |z -i| = 1