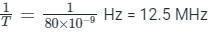Test: Asynchronous Counter - 1 - Electrical Engineering (EE) MCQ
10 Questions MCQ Test - Test: Asynchronous Counter - 1
The maximum clock frequency in MHz of a 4-stage ripple counter, utilizing flip-flops, with each flip-flop having a propagation delay of 20 ns, is ___________. (round off to one decimal place)
The number of T flip-flops required to realise a mod-10 asynchronous counter is:
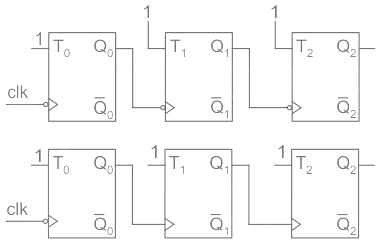
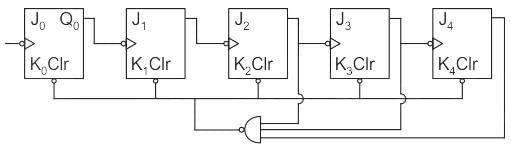
What is the mod number of asynchronous counter shown (All J = K = 1) below:

Propagation delay of flip flops used for counter design largely affects the speed of operation of
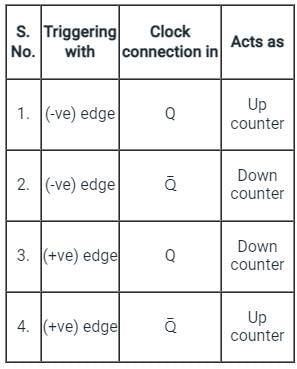
A ripple counter with n flip-flops can function as a
Which shift register counter required the most decoding circuitry?
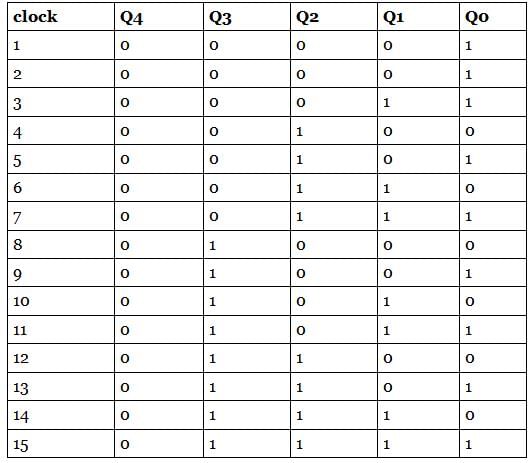
The number of J-K flip flops in modulo 16 binary up-counter are:
An 8-bit ripple counter and an 8 bit synchronous counter are made using flip flops having a propagation delay of 10 ns each. If the worst-case delay in the ripple counter and the synchronous counter be R and S respectively, then
Minimum number of flip flops required for Modulus 15 counter is