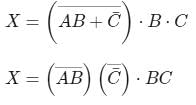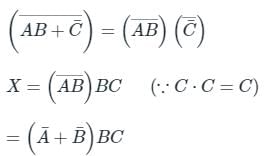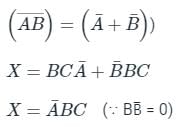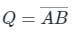Test: Logic Gates & Boolean Algebra - 1 - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test - Test: Logic Gates & Boolean Algebra - 1
Consider a Boolean gate (D) where the output Y is related to the inputs A and B as, Y = A + B̅, where + denotes logical OR operation. The Boolean inputs ‘0’ and ‘1’ are also available separately. Using instances of only D gates and inputs ‘0’ and ‘1’, __________ (select the correct option(s)).
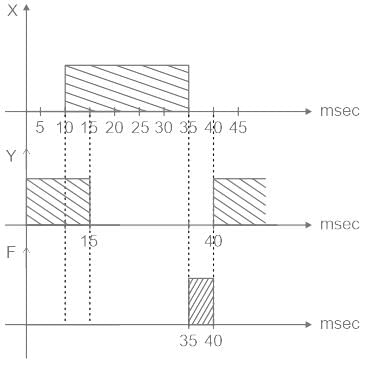
For the given digital circuit. NOT gate is having a time delay of 5 msec. Find for which time range the LED will glow up.
X input is logic 1 for 10 msec to 35msec as shown in the figure. (logic 1 is considered as 5 V and logic 0 as 0 V)
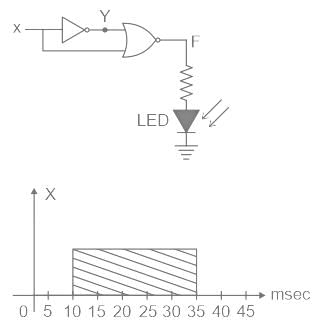
X input is logic 1 for 10 msec to 35msec as shown in the figure. (logic 1 is considered as 5 V and logic 0 as 0 V)

The Boolean equation X = [(A + B̅) (B + C)] B can be simplified to
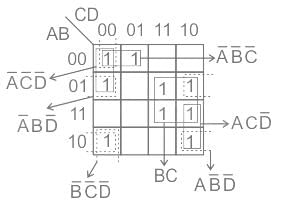
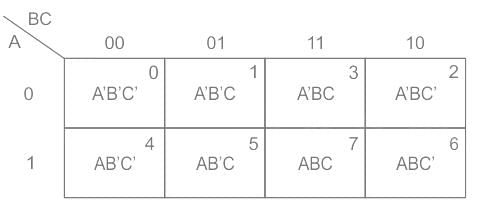
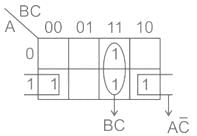
Identify the number of prime implicants and essential prime implicants for the function
f(A, B, C, D) = Σ m(0, 1, 4, 6, 7, 8, 10, 14, 15)
(where m represents min terms)
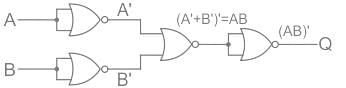
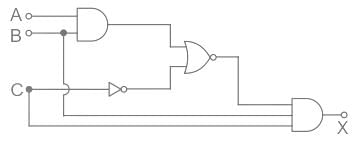
Find the output Boolean function for the logic circuit.
If the Boolean expression P̅Q + QR + PR is minimized, the expression becomes:
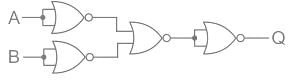
The output of logic circuit given below represents _______ gate.
Simplify the following expression.
Y = AB + A(B + C) + B(B + C)
The Boolean expression AB + AC̅ + BC simplifies to
The minterm expansion of f (P, Q, R) = PQ + QR̅ + PR̅ is