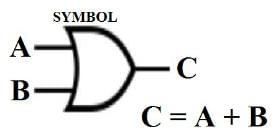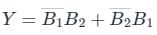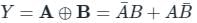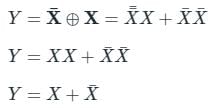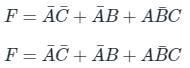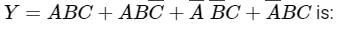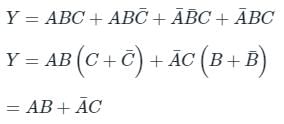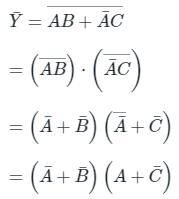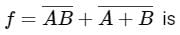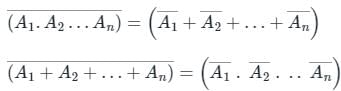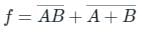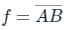Test: Logic Gates & Boolean Algebra - 2 - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test - Test: Logic Gates & Boolean Algebra - 2
Select the Boolean function(s) equivalent to x + yz, where x, y, and z are Boolean variables, and + denotes logical OR operation.
Given below are two statements:
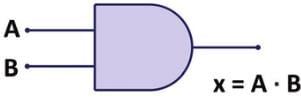
Statement I: A two-input OR gate and a two-input AND gate have similar inputs. but outputs may be the same or different.
Statement II: An AND gate has inputs A and B. The input B is always low, the state of input A can affect the output.
In the light of the above statements, choose the correct answer from the options given below:
Statement I: A two-input OR gate and a two-input AND gate have similar inputs. but outputs may be the same or different.
Statement II: An AND gate has inputs A and B. The input B is always low, the state of input A can affect the output.
In the light of the above statements, choose the correct answer from the options given below:
Four statements are given below. Identify the correct statement.
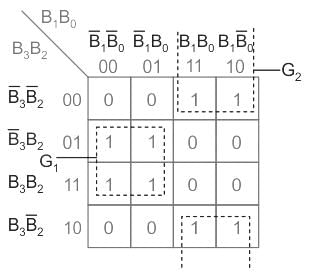
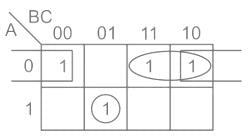
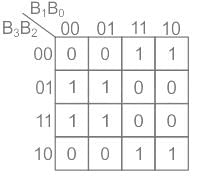
Write the simplified equation for the given K-Map.
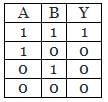
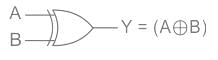
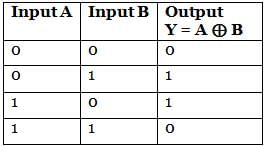
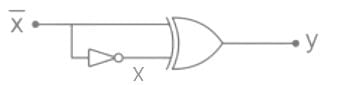
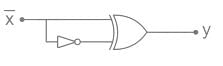
The output Y of the logic circuit given below is:-
Which one of the following gives the simplified sum of products expression for the Boolean function F = m0 + m2 + m3 + m5, where m0, m2, m3 and m5 are minterms corresponding to the inputs A, B and C and A as the MSB and C as the LSB?