Test: Miller Effect Capacitance - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test - Test: Miller Effect Capacitance
Find net voltage gain, given hfe = 50 and hie = 1kΩ.


Consider an RC coupled amplifier at low frequency. Internal voltage gain is -120. Find the voltage gain magnitude, when given that collector resistance = 1kΩ, load = 9kΩ, collector capacitance is 0. is 0.1μF, and input frequency is 20Hz.
Given collector resistance = 2kΩ, load resistance = 5kΩ, collector capacitance = 1μF, emitter capacitance = 20μF, collector current = 2mA, source resistance = 2kΩ. If the effect of blocking capacitor is ignored, find the applicable cut-off frequency.
What is the phase shift in RC coupled CE amplifier at lower 3dB frequency?
When applying miller’s theorem to resistors, resistance R1 is for node 1 and R2 for node 2. If R1>R2, then for same circuit, then for capacitance for which the theorem is applied, which will be larger, C1 or C2?
Given that capacitance w.r.t the input node is 2pF and output node is 4pF, find capacitance between input and output node.
Find the 3-dB frequency given that the gain of RC coupled amplifier is 150, the low frequency voltage gain is 100 and the input frequency is 50Hz.
Consider the circuit shown.
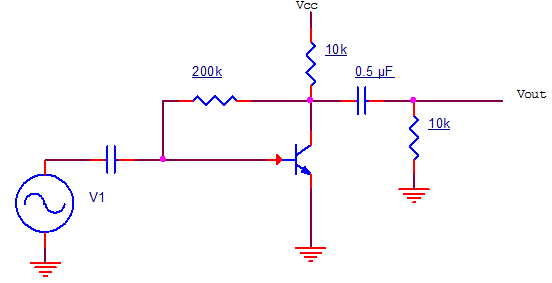
hfe = 50, hie = 1000Ω. Find magnitude of voltage gain at input frequency 10Hz.
Consider that the phase shift of an RC coupled CE amplifier is 260°. Find the low frequency gain when the voltage gain of the transistor is -150.



















