Test: Numericals on Unit Cells Dimensions - Chemistry MCQ
10 Questions MCQ Test - Test: Numericals on Unit Cells Dimensions
Rubidium Chloride (RbCl) has NaCl like structure at normal pressures. If the radius of the Chloride ion is 1.54 Å, what is the unit cell edge length for RbCl? (Assuming anion-anion contact)
A metal crystallizes into two cubic phases BCC and FCC. The ratio of densities of FCC and BCC is equal to 1.5. Calculate the difference between the unit cell lengths of the FCC and BCC crystals if the edge length of the FCC crystal is equal to 4.0 Å.
The radius of an atom of an element is 55 pm. What is the edge length of the unit cell if it is body-centred cubic?
Lithium forms a BCC lattice with an edge length of 350 pm. The experimental density of lithium is 0.53 g cm-3. What is the percentage of missing lithium atoms? (Atomic mass of Lithium = 7 amu)
Gold (atomic mass 197 u) crystallises in a face-centred unit cell. What is its atomic radius if the edge length of the gold unit cell is 0.407 x 10-9m?
If the radius of a Chloride ion is 0.154 nm, then what is the maximum size of a cation that can fit in each of its octahedral voids?
An element of density 8.0 g/cm3 forms an FCC lattice with unit cell edge of 300 pm. Calculate the number of atoms present in 0.5kg of the element.
An element with cell edge of 288 pm has a density of 7.2 g cm-3. What type of structure does the element have if it’s atomic mass M=51.8 g mol-1?
A metal X has a BCC structure with nearest neighbor distance 365.9 pm. What is metal X if its density is 1.0016 g cm-3?
Aluminium crystallises in a face-centred cubic lattice. The edge length of the unit cell of aluminium is 4.05 x 10-10m. What is the density of aluminium? (Atomic mass of Al=27)



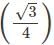 x a
x a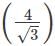 x r= 4 x 55/1.732 = 127 pm.
x r= 4 x 55/1.732 = 127 pm.
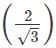 x d = 2/1.732 x 365.9 = 422.5 pm
x d = 2/1.732 x 365.9 = 422.5 pm















