Test: Crystal Lattices and Unit Cells - Chemistry MCQ
15 Questions MCQ Test - Test: Crystal Lattices and Unit Cells
If a metal forms a FCC lattice with unit edge length 500 pm. Calculate the density of the metal if its atomic mass is 110.
How many parameters are used to characterize a unit cell?
If the aluminum unit cell exhibits face-centered behavior then how many unit cells are present in 54g of aluminum?
Atoms of element X form a BCC and atoms of element Y occupy 3/4th of the tetrahedral voids. What is the formula of the compound?
Identify the dimensional relation for the unit cell illustrated below.

If a crystal lattice has 6 closed-pack spheres, what the number of tetrahedral voids in the lattice?
What is the coordination number of a body-centered unit cell?
Which of the following is regarded as the ‘repeatable entity’ of a 3D crystal structure?
What is each point (position of particle) in a crystal lattice termed as?
What is the radius of a metal atom if it crystallizes with body-centered lattice having a unit cell edge of 333 Pico meter?
What is the total volume of the particles present in a body centered unit cell?
A compound is formed by atoms of elements A occupying the corners of the unit cell and an atom of element B present at the center of the unit cell. Deduce the formula of the compound.
Which of the following possess anisotropic nature within their structure?
Which of the following arrangements of particles does a simple cubic lattice follow?
Which of the following unit cells has constituent particles occupying the corner positions only?


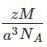
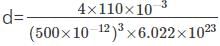 =5846 kg/m3.
=5846 kg/m3.
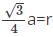
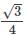 x 333 pm = 144.19 pm is the radius of the metal atom.
x 333 pm = 144.19 pm is the radius of the metal atom.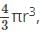 total volume of all particles in BCC =
total volume of all particles in BCC = 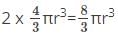 since a BCC has 2 particles per cell.
since a BCC has 2 particles per cell.















