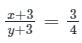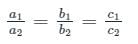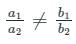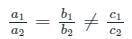Test: Linear Equations in Two Variables - 2 - Class 10 MCQ
15 Questions MCQ Test - Test: Linear Equations in Two Variables - 2
If 8a2b = 27, ab2 = 216, find the value of ab.
If a2 + b2 = 4b + 6a – 13, then what is the value of a + b?
If the equations 14x + 8y + 5 = 0 and 21x - ky - 7 = 0 have no solution, then the value of k is:
Cost of 8 pencils, 5 pens and 3 erasers is Rs. 111. Cost of 9 pencils, 6 pens and 5 erasers is Rs. 130. Cost of 16 pencils, 11 pens and 3 erasers is Rs. 221. What is the cost (in Rs) of 39 pencils, 26 pens and 13 erasers?
If 8k6 + 15k3 – 2 = 0, then the positive value of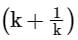 is:
is:
X attempts 100 questions and gets 340 marks. If for every correct answer is 4 marks and wrong answer is negative one mark, then the number of questions wrongly answered by Mr. X is:
A piece of cloth costs Rs. 35. If the piece were 4 m longer and each meter was to cost Rs. 1 lesser, then the total cost would remain unchanged. How long is the piece of cloth?
The denominator of a fraction is 2 more than its numerator. If 3 is added to the numerator and denominator, the fraction becomes 3/4. What was the original fraction?
If (a + b)2 − 2(a + b) = 80 and ab = 16, then what can be the value of 3a − 19b?
The sum of two positive numbers is 14 and difference between their squares is 56. What is the sum of their squares?
Three cups of ice cream, two burgers and four soft drinks together cost Rs. 128. Two cups of ice cream, one burger and two soft drinks together cost Rs. 74. What is the cost of five burgers and ten soft drinks?
The difference between two numbers is 5. If 25 is subtracted from the smaller number and 20 is added to the greater number the ratio becomes 1 : 2. What is the greater number?
If the system of equations 2x + 3y = 5, 4x + ky = 10 has infinitely many solutions then k =?
The sum of two numbers is 184. If one-third of one exceeds one-seventh of the other by 8, find the smaller number
The difference between a two-digit number and the number obtained by interchanging the positions of its digits is 36. What is the difference between the two digits of that number?