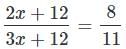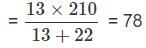Test: Ratio & Proportion - Grade 10 MCQ
15 Questions MCQ Test - Test: Ratio & Proportion
The sum of 3 numbers is 285. Ratio between 2nd and 3rd numbers is 6 ∶ 5. Ratio between 1st and 2nd numbers is 3 ∶ 7. The 3rd number is?
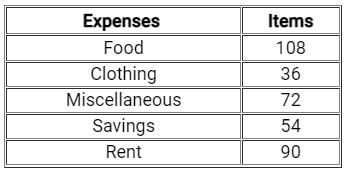
The ratio of average of expenses on food, clothing and miscellaneous items to the average of expenses on savings and rent is

A man has 25 paise, 50 paise and 1 Rupee coins. There are 220 coins in all and the total amount is 160. If there are thrice as many 1 Rupee coins as there are 25 paise coins, then what is the number of 50 paise coins?
If a : b = 3 : 2, b : c = 2 : 1, c : d = 1/3 : 1/7 and d : e = 1/4 : 1/5 find a : b : c : d : e.
u : v = 4 : 7 and v : w = 9 : 7. If u = 72, then what is the value of w?
A diamond weighing 35 grams cost Rs. 12,250 is cut down into two pieces having weights in the ratio of 5 ∶ 2. If the price directly proportional to the square of the weight then find the loss incurred.
In a bag, there are coins of 5ps, 10ps, and 25ps in a ratio of 3 : 2 : 1. If there are Rs. 60 in all, how many 5ps coins are there?
Rs.750 are divided among A, B and C in such a manner that A : B is 5 : 2 and B : C is 7 : 13. What is A’s share?
In a family, the age of father, mother, son, and grandson are A, B, C, and D respectively. Given that A - B = 3, B + C = 78, C + D = 33 and the average age of the family is 34 years, then (B - C) is:
The monthly salaries of A and B are in the ratio 5 : 6. If both of them get a salary increment of Rs. 2000, the new ratio becomes 11 : 13. What is the new monthly salary of A?
Rahul has a bag which contains Rs. 1, 50 paisa, and 25 paisa coins and the ratio of number of coins is 1 ∶ 1/2 ∶ 1/3. If Rahul has a total amount of Rs 1120, then find the total value of 25 paisa coins.
A man divided an amount between his sons in the ratio of their ages. The sons received Rs. 54000 and Rs. 48000. If one son is 5 years older than the other, find the age of the younger son.
The number of students in 3 classes is in the ratio 2 : 3 : 4. If 12 students are increased in each class this ratio changes to 8 : 11 : 14. The total number of students in the three classes in the beginning was
A box has 210 coins of denominations one-rupee and fifty paise only. The ratio of their respective values is 13 : 11. The number of one-rupee coin is