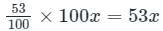Test: Percentages - 2 - Grade 10 MCQ
15 Questions MCQ Test - Test: Percentages - 2
A glass of juice contains 5% fruit extract, 25% of pulp and rest of water. Find amount of water that should be added in glass of 450 ml juice to reduce pulp concentration to 15%?
A solution contains 33g of common salt in 320g of water. Calculate the concentration in terms of mass, by mass percentage of the solution.
In an election A got 55% of the total votes and the remaining votes were casted to B. If 10,000 votes of A are given to B, there would have been a tie. Find the number of total votes polled?
There were two candidates in an election, 10% of voters did not vote and 48 votes were found invalid. The winning candidate got 53% of all the voters in the list and won by 304 votes. Find the total number of votes enrolled.
65% of a number is more than 25% of the number by 120. What is 20% of that number?
If the price of petrol has increased from Rs. 40 per litre to Rs. 60 per litre, by how much percent a person has to decrease his consumption so that his expenditure remains same.
Out of two numbers, 65% of the smaller number is equal to 45% of the larger number. If the sum of two numbers is 2574, then what is the value of the larger number?
If the average, of a given number, 50% of that number and 25% of the same number is 280, then the number is
Two students appeared for an examination. One of them secured 22 marks more than the other and his marks were 55% of the sum of their marks. The marks obtained by them are _______.
A fruit seller sells 45% of the oranges that he has along with one more orange to a customer. He then sells 20% of the remaining oranges and 2 more oranges to a second customer. He then sells 90% of the now remaining oranges to a third customer and is still left with 5 oranges. How many oranges did the fruit seller have initially?
5%-income of A is equal to 15% income of B and 10% income of B is equal to 20% income of C. If income of C is Rs. 2,000, then the sum of incomes (in Rs.) of A, B and C is:
A furniture company imported three types of woods, Wood A worth Rs. 440000, Wood B worth Rs. 230000 and Wood C worth Rs. 190000. Company had to pay 15% duty on Wood A, 9% on Wood B and 7% on Wood C. How much total duty (in rupees) Company had to pay on all items?
If a number x is 10% less than another number y and y is 10% more than 125, then the value of x is:
In the beginning of 2020, the population of three cities 'A', 'B', and 'C' was in the ratio of 4 : 5 : 6 respectively. During the year 2021, the population of respective cities increased by a percentage in the ratio of 7 : 5 : 9. In the beginning of 2021, the population of city 'C' was 27000 more than that of the beginning of the year 2020 and in the beginning of the year 2021 the ratio of the population of A : B was 108 : 125 then during the year 2020, what was the sum of the increase in the population of all the cities together?
Monthly income of a person was Rs. 36,000. if he spent 25% on food, 12 % on his children's education and saves x% in bank account. After the calculation, he found that he was left with Rs. 2160. Find the sum of amount which he saves in his bank.