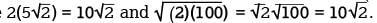Test (No calculator) - 2 - SAT MCQ
10 Questions MCQ Test - Test (No calculator) - 2
b = 2.35 + 0.25x
c = 1.75 + 0.40x
In the equations above, b and c represent the price per pound, in dollars, of beef and chicken, respectively, x weeks after July 1 during last summer. What was the price per pound of beef when it was equal to the price per pound of chicken?
c = 1.75 + 0.40x
In the equations above, b and c represent the price per pound, in dollars, of beef and chicken, respectively, x weeks after July 1 during last summer. What was the price per pound of beef when it was equal to the price per pound of chicken?
A line in the xy-plane passes through the origin and has a slope of 1/7. Which of the following points lies on the line?
If (ax + 2)(bx + 7) = 15x2 + cx + 14 for all values of x, and a + b = 8, what are the two possible values for c?
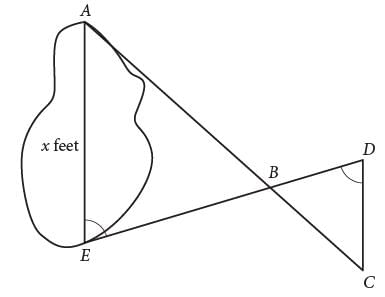
A summer camp counselor wants to find a length, x, in feet, across a lake as represented in the sketch above. The lengths represented by AB, EB, BD, and CD on the sketch were determined to be 1800 feet, 1400 feet, 700 feet, and 800 feet, respectively.
Segments AC and DE intersect at B, and ∠AEB and ∠CDB have the same measure. What is the value of x?
x + y = -9
x + 2y = -25
According to the system of equations above, what is the value of x?
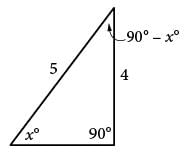
In a right triangle, one angle measures x °, where sin x ° = 4/5. What is cos (90° − x°)?



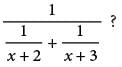
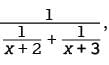 multiply by
multiply by  ThiS results in the expression
ThiS results in the expression  Which
Which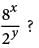
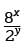 so that the numerator and denominator are expressed with the same base. Since 2 and 8 are both powers of 2, substituting 23 for 8 in the numerator
so that the numerator and denominator are expressed with the same base. Since 2 and 8 are both powers of 2, substituting 23 for 8 in the numerator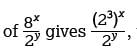 which can be rewritten as
which can be rewritten as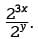 Since the numerator and denominator of
Since the numerator and denominator of  have a common base, this expression can be rewritten as 23x-y. It is given that 3x - y = 12, so one can substitute 12 for the exponent, 3x - y, given that the expression
have a common base, this expression can be rewritten as 23x-y. It is given that 3x - y = 12, so one can substitute 12 for the exponent, 3x - y, given that the expression 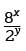 is equal to 212.
is equal to 212.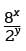 can be rewritten as
can be rewritten as 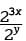 , or 23x-y. If the value of 23x-y is 44, which can be rewritten as 28, then 23x-y = 28, which results in 3x - y = 8, not 12. Choice C is incorrect. If the value of
, or 23x-y. If the value of 23x-y is 44, which can be rewritten as 28, then 23x-y = 28, which results in 3x - y = 8, not 12. Choice C is incorrect. If the value of  which results in 3x - y = 6, not 12.
which results in 3x - y = 6, not 12.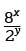 can be determined.
can be determined. Substituting the given values of 800 for CD, 700 for BD, and 1400 for EB in
Substituting the given values of 800 for CD, 700 for BD, and 1400 for EB in 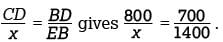 Therefore,
Therefore, 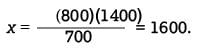
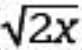 , what is the value of x?
, what is the value of x?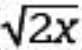 , giving 10√2 =
, giving 10√2 = 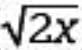 . Squaring each side of 10√2 =
. Squaring each side of 10√2 = 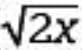 gives
gives 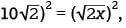 which simplifies to
which simplifies to 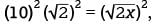 or 200 = 2x. This gives x = 100. To verify, substitute 100 for x and 5√2 for a in the equation 2a = √2x, which yields 2(5√2) =
or 200 = 2x. This gives x = 100. To verify, substitute 100 for x and 5√2 for a in the equation 2a = √2x, which yields 2(5√2) = 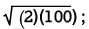 this is true since
this is true since