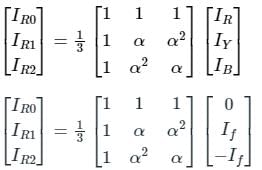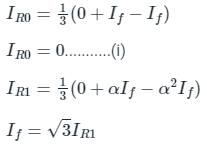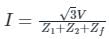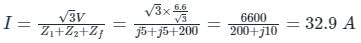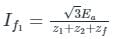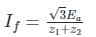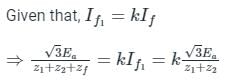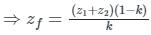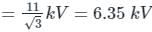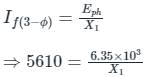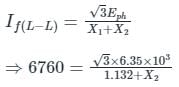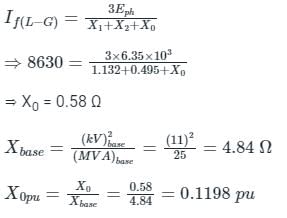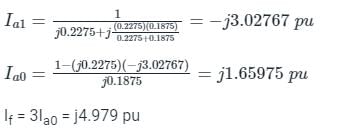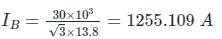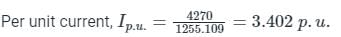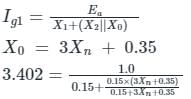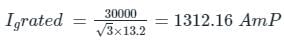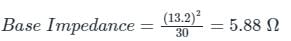Test: Line to Line & Double Line to Ground Fault - Electrical Engineering (EE) MCQ
10 Questions MCQ Test - Test: Line to Line & Double Line to Ground Fault
In which type of fault, zero sequence currents do not exist?
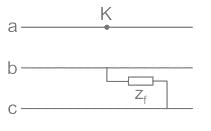
At the terminal of a 3ϕ, 6.6 kV, 10 MVA alternator, a load R = 200 Ω is connected between two phases, and other phase is kept open. The sequence impedance of the alternator is Z1 = Z2 = j 5Ω and Z0 = j2Ω.
What is the current through the load resistance?
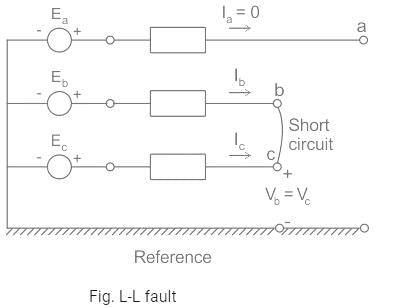
In a three phase system for a line to line fault the positive, negative and zero sequence voltage Va1, Va2, Va0 respectively, for phase voltage Va are related as
The positive, negative and zero sequence impedances of a three-phase generator are Z1, Z2 and Z0 respectively. For a line-to-line fault with fault impedance Zf, the fault current is If1 = kIf, where If is the fault current with zero fault impedance. The relation between Zf and k is
An 11 kV, 25 MVA, 3-phase Y-connected alternator was subjected to three different types of fault at its terminals. The fault currents were:
5610 A for a three phase fault
6760 A for line to line fault
8630 A for single line to ground fault.
If the alternator neutral is solidly grounded, the zero-sequence reactance of the alternator (in pu) is _________
Determine the fault current in the system following a double line to ground short circuit fault at the terminal of a star connected synchronous generator operating initially on an open circuit voltage of 1.0 pu. The positive, negative, and zero sequences reactance of the generator are, respectively j0.35, j0.25, and j0.20, and the star point is isolated from the ground.
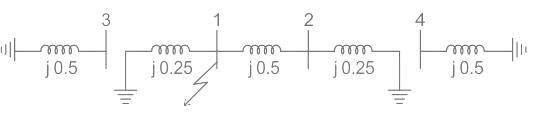
The reactance data for a power system is shown in the figure in per unit on a common base is as follows.
G1: X1 = X2 = j0.1, X0 = j0.05
G2: X1 = X2 = j0.1, X0 = j0.05
T1: X1 = X2 = j0.25, X0 = j0.25
T2: X1 = X2 = j0.25, X0 = j0.25
Line: X1 = X2 = j0.3, X0 = j0.5
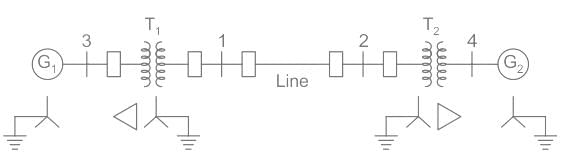
If a double line to ground fault occurs at bus 1, the fault current is _______
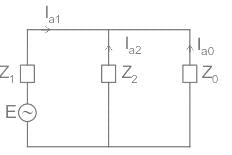
A 30 MV A, 3-phase, 50Hz,13.8kV, star-connected synchronous generator has positive, negative and zero sequence reactances, 15%,15% and 5% respectively. A reactance (Xn) is connected between the neutral of the generator and ground. A double line to ground fault takes place involving phases ′b′and′c′, with a fault impedance of j0.1p.u. The value of Xn (in p.u.) that will limit the positive sequence generator current to 4270 A is _________.
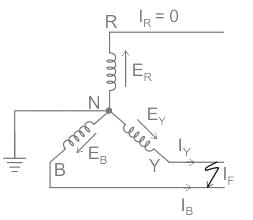
A three-phase star-connected alternator rated at 30 MVA, 13.8 kV has positive, negative, and zero sequence reactance values as 0.25 pu, 0.35 pu, and 0.10 pu respectively. The neutral of the alternator is solidly grounded. Find the current in phase B when a double line to ground fault occurs on its terminals B and C.
A 30 MVA, 13.2 KV synchronous generator has solid grounded neural. It positive, negative and zero sequence impedance are 0.30, 0.40 and 0.05 PU respectively. What value of reactance (in ohm) must be placed in the neutral of the generator to restrict the fault current to ground to rated line current for a double line to ground fault.