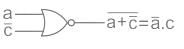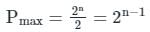Test: Minimization of Boolean Functions - 1 - Computer Science Engineering (CSE) MCQ
10 Questions MCQ Test - Test: Minimization of Boolean Functions - 1
The following function F= AB'CD' +A'BCD' +AB'C'D+A'BC'D is realized using 2 input EX-OR and AND gates. The number of EX-OR gates and AND Gates required to implement the function respectively are?
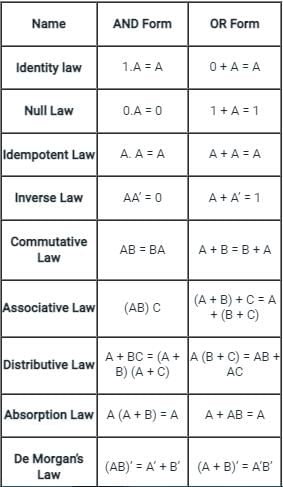
Which of the is sufficient to represent any boolean operation.
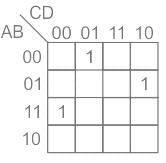
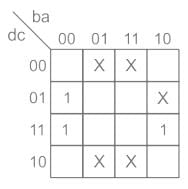
Consider the Karnaugh map given below. Where X represents “don’t care” and blank represents 0.
Assume for all inputs (a, b, c, d), the respective complements (a̅, b̅, c̅, d̅) are also available. The above logic is implemented using 2-input NOR gates only. The minimum number of gates required is ________.
The number of essential prime implicants for the Function Y = A'B'C'D + A'BCD' + ABC'D' is given by ______
For an n-variable Boolean function, the maximum number of prime implicants is
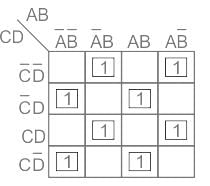
What will be the simplified Boolean function of the given equation?
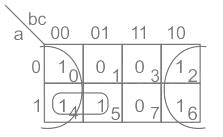
F(a, b, c) = ∑(0, 2, 4, 5, 6)
Solve the following Boolean expression:
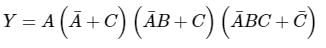
Select the correct option.
Determine the minimised expression of Boolean function
F = X̅ Z̅ + Y̅ Z̅ + Y Z̅ + XYZ