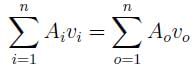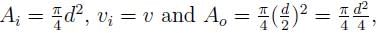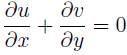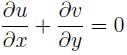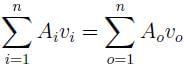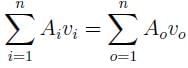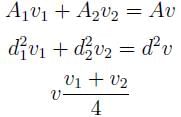All Courses
Get the App Signup / Login
Sign in Open App
Civil Engineering (CE) Exam  >  Civil Engineering (CE) Tests  >  Test: Continuity Equation - Civil Engineering (CE) MCQ

Test: Continuity Equation - Civil Engineering (CE) MCQ


Test Description

10 Questions MCQ Test - Test: Continuity Equation

Test: Continuity Equation for Civil Engineering (CE) 2024 is part of Civil Engineering (CE) preparation. The Test: Continuity Equation questions and answers have been prepared according to the Civil Engineering (CE) exam syllabus.The Test: Continuity Equation MCQs are made for Civil Engineering (CE) 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Continuity Equation below.
Solutions of Test: Continuity Equation questions in English are available as part of our course for Civil Engineering (CE) & Test: Continuity Equation solutions in Hindi for Civil Engineering (CE) course. Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free. Attempt Test: Continuity Equation | 10 questions in 30 minutes | Mock test for Civil Engineering (CE) preparation | Free important questions MCQ to study for Civil Engineering (CE) Exam | Download free PDF with solutions
Test: Continuity Equation - Question 1
Save

If a liquid enters a pipe of diameter d with a velocity v, what will it’s velocity at the exit if the diameter reduces to 0.5d?

Detailed Solution for Test: Continuity Equation - Question 1

According to the Continuity Equation,

where a represents flow area, v represents flow velocity, i is for inlet conditions and o is for outlet conditions.
If, 
vo = 4v

Test: Continuity Equation - Question 2
Save

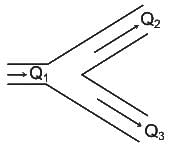
Two pipes, each of diameter d, converge to form a pipe of diameter D. What should be the relation between d and D such that the flow velocity in the third pipe becomes double of that in each of the two pipes?

1 Crore+ students have signed up on EduRev. Have you? Download the App
Test: Continuity Equation - Question 3
Save

In a two dimensional flow, the component of the velocity along the X-axis and the Y-axis are u = ax2 + bxy + cy2 and v = cxy. What should be the condition for the flow field to be continuous?

Detailed Solution for Test: Continuity Equation - Question 3

According to the condition for continuity,

2ax + cx = 0
2a + c = 0.

Test: Continuity Equation - Question 4
Save

In a two dimensional flow, the component of the velocity along the X-axis and the Y-axis are u = ax2 + bxy and v = bxy + ay2. The condition for the flow field to be continuous is
Detailed Solution for Test: Continuity Equation - Question 4

The condition for the flow field to be continuous is:

2ax + by + 2ay + bx = 0
x + y = 0
Hence, the condition for the flow field to be continuous is independent of the constants (a; b) and dependent only on the variables (x; y).

Test: Continuity Equation - Question 5
Save

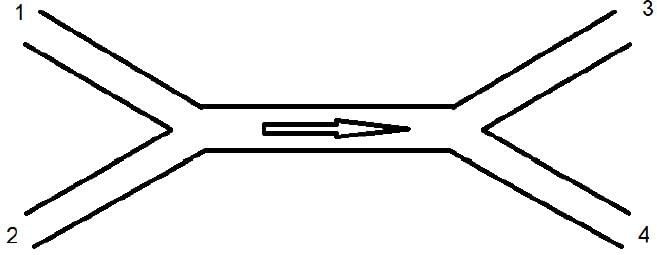
In a water supply system, water flows in from pipes 1 and 2 and goes out from pipes 3 and 4 as shown. If all the pipes have the same diameter, which of the following must be correct?
Detailed Solution for Test: Continuity Equation - Question 5

According to the Continuity Equation,

where a represents flow area, v represents flow velocity, i is for inlet conditions and o is for outlet conditions.
A1v1 + A2v2 = A3v3 + A4v4
Since d1 = d2 = d3 = d4, v1 + v2 = v3 + v4.

Test: Continuity Equation - Question 6
Save

The continuity equation is based on the principle of
Detailed Solution for Test: Continuity Equation - Question 6

According to the Continuity Equation, if no fluid is added or removed from the pipe in any length then the mass passing across different sections shall be the same. This is in accordance with the principle of conservation of mass which states that matter can neither be created nor be destroyed.

Test: Continuity Equation - Question 7
Save

Two pipes of diameters d1 and d2 converge to form a pipe of diameter 2d. If the liquid flows with a velocity of v1 and v2 in the two pipes, what will be the flow velocity in the third pipe?
Detailed Solution for Test: Continuity Equation - Question 7

According to the Continuity Equation,


where a represents flow area, v represents flow velocity, i is for inlet conditions and o is for outlet conditions. Thus,

Test: Continuity Equation - Question 8
Save

St. venant equations represent
Detailed Solution for Test: Continuity Equation - Question 8

St. Venant Equations:
1. Continuity equation

2. Momentum Equation

Assumptions for St. Venant Equations

  • Flow is one-dimensional
  • Hydrostatic pressure prevails and vertical accelerations are negligible
  • Streamline curvature is small.
  • Bottom slope of the channel is small.
  • Manning’s equation is used to describe resistance effects
  • The fluid is incompressible

Hence, St. venant equations represent continuity and momentum equations.

Test: Continuity Equation - Question 9
Save

A fluid flowing through a pipe of diameter 450 mm with velocity 3 m/s is divided into two pipes of diameters 300 mm and 200 mm. The velocity of flow in 300 mm diameter pipe is 2.5 m/s, then the velocity of flow through 200 mm diameter pipe will be 
Detailed Solution for Test: Continuity Equation - Question 9

Concept:
According to continuity, the liquid flow rate will be conserved.
Q1 = Q2 + Q3
In a pipe, flow rate is given by
Q = AV
Calculation:
Given V1 = 3 m/s, D1 = 450 mm, V2 = 2.5 m/s, D2 = 300 mm, D3 = 200 mm;
From continuity,
D12 V1 = D22 V2 + D32 V3
⇒ 4502 × 3 = 3002 × 2.5 + 2002 × V3
⇒ V3 = 9.56 m/s 

*Answer can only contain numeric values
Test: Continuity Equation - Question 10
Save

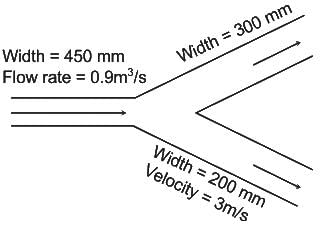
A channel of width 450 mm branches into two sub-channels having width 300 mm and 200 mm as shown in figure. If the volumetric flow rate (taking unit depth) of an incompressible flow through the main channel is 0.9 m3/s and the velocity in the sub-channel of width 200 mm is 3 m/s, the velocity in the sub-channel of width 300 mm is ______m/s
Assume both inlet and otlet to be at the same elevation.

Detailed Solution for Test: Continuity Equation - Question 10


Concept:
The principle used here is Conservation of mass
∴ Q1 = Q2 + Q3
Calculation:
Q1 = Q2 + Q3
A1V1 = A2V2 + A3V3
⇒ 0.9 = 300 × 10-3 × V2 + 200 × 10-3 × 3
⇒ 0.9 = 0.3 V2 + 0.6
⇒ V2 = 1 m/s

Information about Test: Continuity Equation Page
In this test you can find the Exam questions for Test: Continuity Equation solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Continuity Equation, EduRev gives you an ample number of Online tests for practice

Top Courses for Civil Engineering (CE)

Download as PDF

Top Courses for Civil Engineering (CE)

Important Questions for Continuity Equation

Find all the important questions for Continuity Equation at EduRev.Get fully prepared for Continuity Equation with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Continuity Equation syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Continuity Equation resources.

Continuity Equation MCQs with Answers

Prepare for the Continuity Equation within the Civil Engineering (CE) exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Continuity Equation

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Continuity Equation with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup