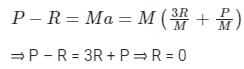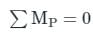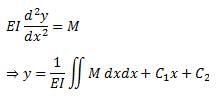Test: Beams - Mechanical Engineering MCQ
10 Questions MCQ Test - Test: Beams
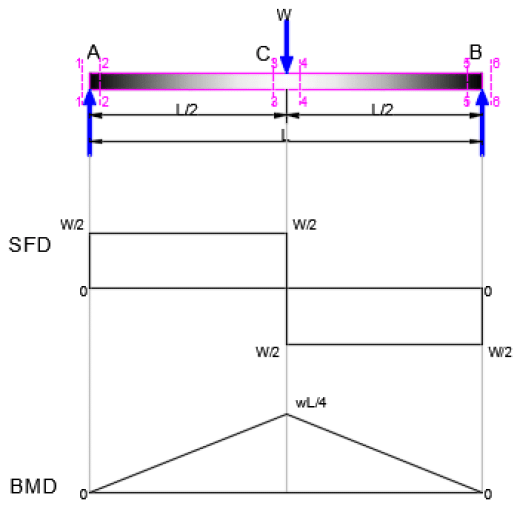
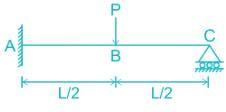
Consider a beam sustaining a load of "L" kN at its center. Which of the following options gives the maximum bending moment of the given beam? (where I is length of beam)
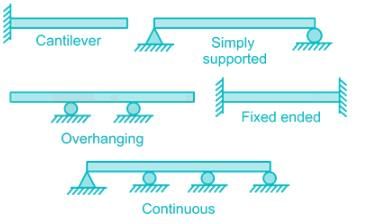
Six fundamental methods of supporting beam are shown below:
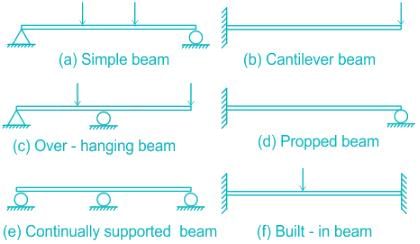
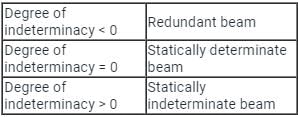
Which cases fall under the category of statically indeterminate beams?
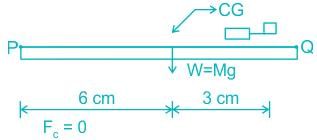
A mobile phone has a small motor with an eccentric mass used for vibrator mode. The location of the eccentric mass on motor with respect to center of gravity (CG) of the mobile and the rest of the dimensions of the mobile phone are shown. The mobile is kept on a flat horizontal surface.
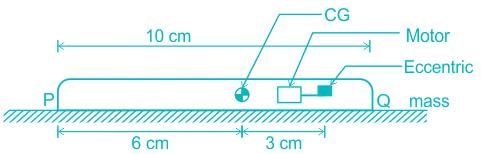
Given in addition that the eccentric mass = 2 grams, eccentricity = 2.19 mm, mass of the mobile = 90 grams, g = 9.81 m/s2. Uniform speed of the motor in RPM for which the mobile will get just lifted off the ground at the end Q is approximately.
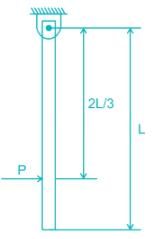
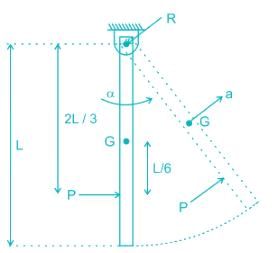
A uniform rigid rod of mass M and length L is hinged at one end as shown in the adjacent figure. A force P is applied at a distance of 2L/3 from the hinge so that the rod swings to the right. The horizontal reaction at the hinge is
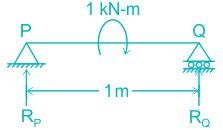
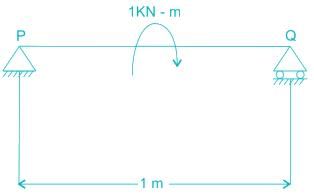
A simply supported beam PQ is loaded by a moment of 1 kN-m at the mid-span of the beam as shown in the figure. The reaction forces RP and RQ at supports P and Q respectively are
A simply supported laterally loaded beam was found to deflect more than a specified value. Which of the following measures will reduce the deflection?
The area moment of inertia of a square of size 1 unit about its diagonal is


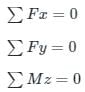




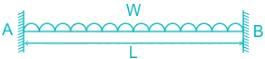
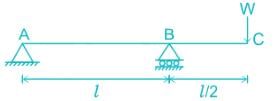
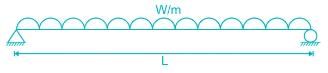
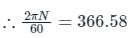
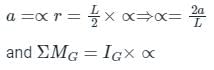
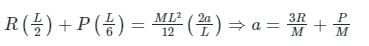 ...(1)
...(1)