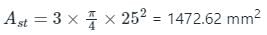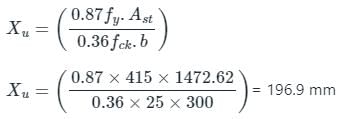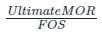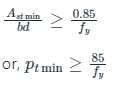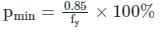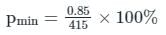Civil Engineering (CE) Exam > Civil Engineering (CE) Tests > Test: Beam - Civil Engineering (CE) MCQ
Test: Beam - Civil Engineering (CE) MCQ
Test Description
10 Questions MCQ Test - Test: Beam
Test: Beam for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Test: Beam questions and answers have been prepared
according to the Civil Engineering (CE) exam syllabus.The Test: Beam MCQs are made for Civil Engineering (CE) 2025 Exam.
Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Beam below.
Solutions of Test: Beam questions in English are available as part of our course for Civil Engineering (CE) & Test: Beam solutions in
Hindi for Civil Engineering (CE) course.
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free. Attempt Test: Beam | 10 questions in 30 minutes | Mock test for Civil Engineering (CE) preparation | Free important questions MCQ to study for Civil Engineering (CE) Exam | Download free PDF with solutions
Detailed Solution for Test: Beam - Question 1
Detailed Solution for Test: Beam - Question 2
Test: Beam - Question 3
What is the working moment of resistance for a beam of width 300 mm and effective depth 450 mm having tension reinforcement 3 - 25 mm dia bars of Fe415 and concrete of Grade M25?
Detailed Solution for Test: Beam - Question 3
Test: Beam - Question 4
Structural members subjected to bending and large axial compressive loads are known as
Detailed Solution for Test: Beam - Question 4
Test: Beam - Question 5
The spacing between two vertical stirrups in a rectangular RCC beam is:
Detailed Solution for Test: Beam - Question 5
Detailed Solution for Test: Beam - Question 6
Test: Beam - Question 7
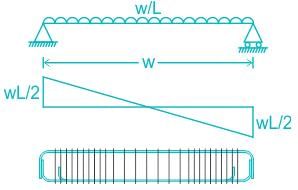
A beam 300 mm depth and of symmetrical I section has a I = 1 x 108 mm4 and is simply supported over a span of 6 m. Calculate the udl it may carry if the max bending stress is not to exceed 100 N/mm2
Detailed Solution for Test: Beam - Question 7
Detailed Solution for Test: Beam - Question 8
Test: Beam - Question 9
The minimum tension reinforcement in beam should not be less than______.
Detailed Solution for Test: Beam - Question 9
Test: Beam - Question 10
What is the minimum area of tension reinforcement in beams when Fe 415 is used?
Detailed Solution for Test: Beam - Question 10
Information about Test: Beam Page
In this test you can find the Exam questions for Test: Beam solved & explained in the simplest way possible.
Besides giving Questions and answers for Test: Beam, EduRev gives you an ample number of Online tests for practice
Download as PDF