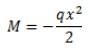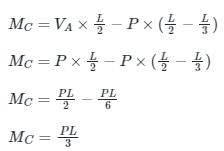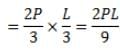Test: Shear Force and Bending Moment - Civil Engineering (CE) MCQ
10 Questions MCQ Test - Test: Shear Force and Bending Moment
The maximum bending moment at 'A' for beam shown in the given figure is given by:

What is the bending moment at end supports of a simply supported beam?
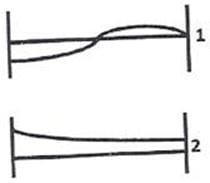
The shapes of the bending moment diagram for a uniform cantilever beam carrying a uniformly distributed load over its length is
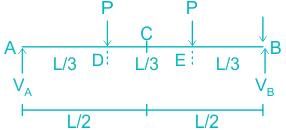
A simply supported beam of span L is subjected to two point loads, each of magnitude P, acting at one third of the span, as shown in the figure below. Which of the follloing statements is correct about the nature of the BMD?
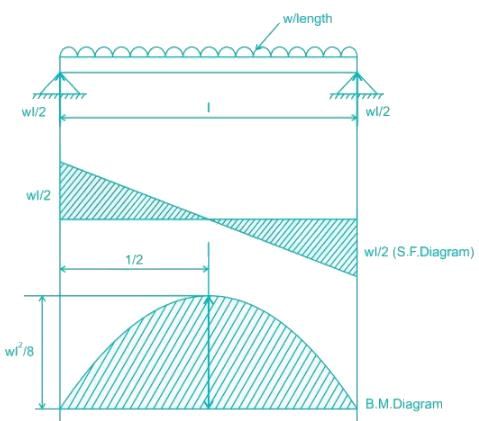
What is the maximum shear force, when a cantilever beam is loaded with udl throughout?
A concentrated load P acts on a simply supported beam of span L at a distance L/3 from the left support. The bending moment at the point of application of the load is given by
What does the slope of a bending moment curve as a function of distance represent?
Sagging, the bending moment occurs at the _____ of the beam.
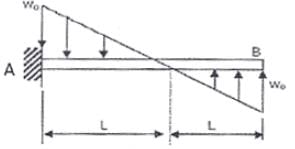
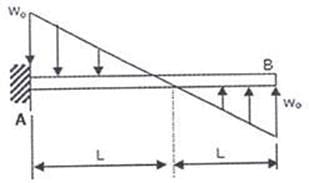
A cantilever beam carriers the anti symmetric load as shown, where w is the peak intensity of the distributed load. Qualitatively, the correct bending moment diagram for the beam is
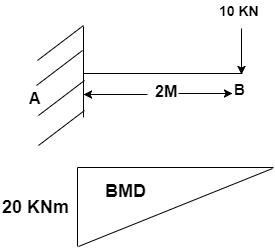
What will be the variation in BMD for the diagram? [Assume l = 2m].
![The variation in BMD for the diagram [Assume l = 2m] is Triangular](https://www.sanfoundry.com/wp-content/uploads/2017/12/strength-materials-questions-answers-shear-force-bending-moment-diagram-q4.png)


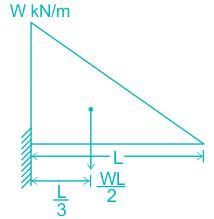
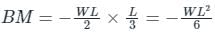 (as per sign convention -ve sign is used)
(as per sign convention -ve sign is used)