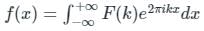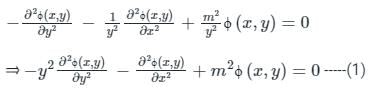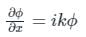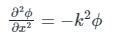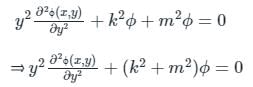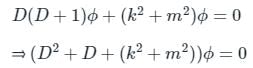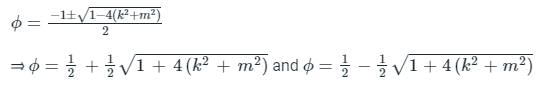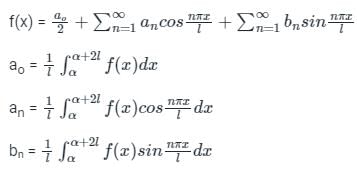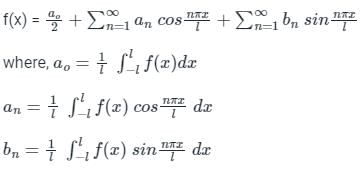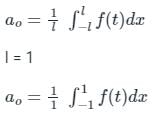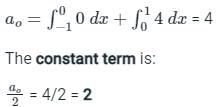Test: Fourier Series - Mechanical Engineering MCQ
10 Questions MCQ Test - Test: Fourier Series
If we use the Fourier transform  to solve the partial differential equation
to solve the partial differential equation  in the half-plane {(x, y) : -∞ < x < ∞, 0 < y < ∞} the Fourier modes ϕk(y) depend on y as yα and yβ. The values of α and β are
in the half-plane {(x, y) : -∞ < x < ∞, 0 < y < ∞} the Fourier modes ϕk(y) depend on y as yα and yβ. The values of α and β are
 to solve the partial differential equation
to solve the partial differential equation  in the half-plane {(x, y) : -∞ < x < ∞, 0 < y < ∞} the Fourier modes ϕk(y) depend on y as yα and yβ. The values of α and β are
in the half-plane {(x, y) : -∞ < x < ∞, 0 < y < ∞} the Fourier modes ϕk(y) depend on y as yα and yβ. The values of α and β are Consider 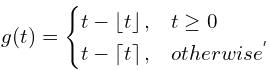 where t ∈ R. Here [t] represents the largest integer less than or equal to t and [t] denotes the samllest integer greater than or equal to t. The coefficient of the second harmonic component of the fourier series representing g(t) is
where t ∈ R. Here [t] represents the largest integer less than or equal to t and [t] denotes the samllest integer greater than or equal to t. The coefficient of the second harmonic component of the fourier series representing g(t) is
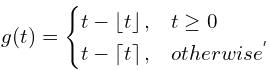 where t ∈ R. Here [t] represents the largest integer less than or equal to t and [t] denotes the samllest integer greater than or equal to t. The coefficient of the second harmonic component of the fourier series representing g(t) is
where t ∈ R. Here [t] represents the largest integer less than or equal to t and [t] denotes the samllest integer greater than or equal to t. The coefficient of the second harmonic component of the fourier series representing g(t) isThe Fourier series expansion of x3 in the interval −1 ≤ x < 1 with periodic continuation has
Let g: [0,∞) → [0,∞) be a function defined by g(x) = x – [x], where [x] represents the integer part of x. (i.e., it is the largest integer which is less than or equal to x). The value of the constant term in the Fourier series expansion of g(x) is
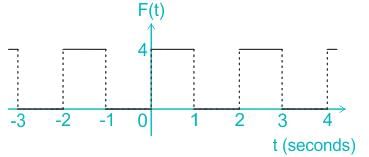
F(t) is a periodic square wave function as shown. It takes only two values, 4 and 0, and stays at each of these values for 1 second before changing. What is the constant term in the Fourier series expansion of F(t)?
What are the conditions called which are required for a signal to fulfil to be represented as Fourier series?
Let x(t) be a periodic signal with time period T, Let y(t) = x(t – to) + x(t + to) for some to. The fourier series coefficients of y(t) are denoted by bk. If bk = 0 for all odd K. Then to can be equal to
Choose the condition from below that is not a part of Dirichlet’s conditions?