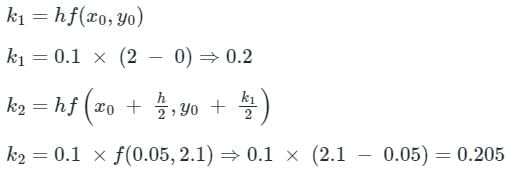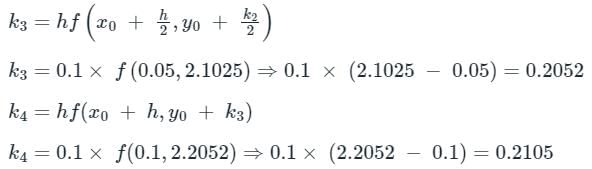Test: Runge Kutta Method - Civil Engineering (CE) MCQ
5 Questions MCQ Test - Test: Runge Kutta Method
If 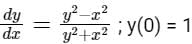 and h = 0.2, then solving by fourth order Runge-Kutta method:
and h = 0.2, then solving by fourth order Runge-Kutta method:
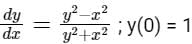 and h = 0.2, then solving by fourth order Runge-Kutta method:
and h = 0.2, then solving by fourth order Runge-Kutta method:Consider the first order initial value problem
y’ = y + 2x – x2, y(0) = 1, (0 ≤ x < ∞) with exact solution y(x) = x2 + ex. For x = 0.1, the percentage diference between the exact solution and the solution obtained using a single iteration of the second-order Runge Kutta method with step size h = 0.1 is
y’ = y + 2x – x2, y(0) = 1, (0 ≤ x < ∞) with exact solution y(x) = x2 + ex. For x = 0.1, the percentage diference between the exact solution and the solution obtained using a single iteration of the second-order Runge Kutta method with step size h = 0.1 is
A gradually varied flow profile can be governed by equation  where x is distance and y is the depth of water above the bed level. Which of the following methods can be used for solution?
where x is distance and y is the depth of water above the bed level. Which of the following methods can be used for solution?
 where x is distance and y is the depth of water above the bed level. Which of the following methods can be used for solution?
where x is distance and y is the depth of water above the bed level. Which of the following methods can be used for solution?Consider an ordinary differential equation 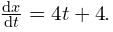 If x = xo at t = 0, the increment in x calculated using Runge Kutta fourth order multistep method with a step size of Δt = 0.2 is
If x = xo at t = 0, the increment in x calculated using Runge Kutta fourth order multistep method with a step size of Δt = 0.2 is
Runge-Kutta fourth order method is used to solve the differential equation 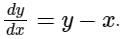 If the initial value y(0) = 2 and step-size is 0.1, then the value of k1, k2, k3, and k4 respectively is?
If the initial value y(0) = 2 and step-size is 0.1, then the value of k1, k2, k3, and k4 respectively is?


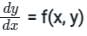 with condition y(x0) = y0
with condition y(x0) = y0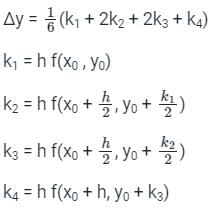
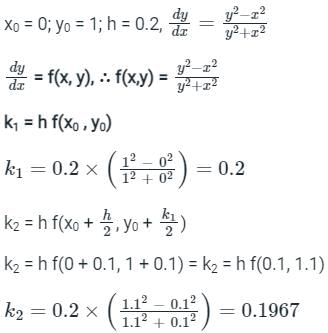

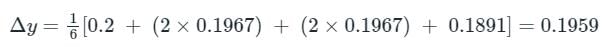

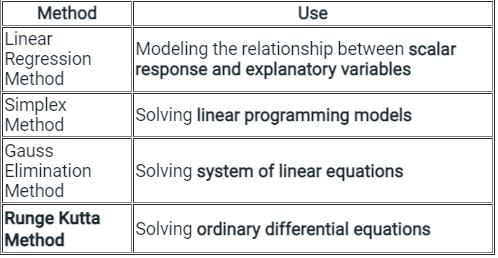
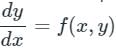 for gradually varied flow profile is an ordinary differential equation.
for gradually varied flow profile is an ordinary differential equation.  is as follows:
is as follows: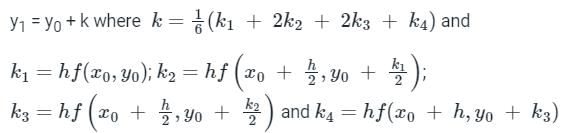
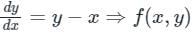 y(0) = 2 and step-size (h) = 0.1
y(0) = 2 and step-size (h) = 0.1