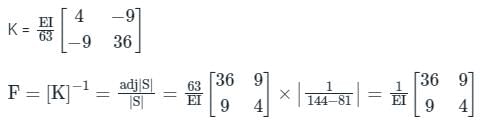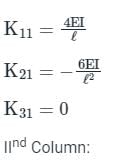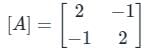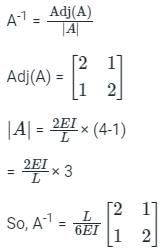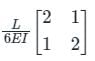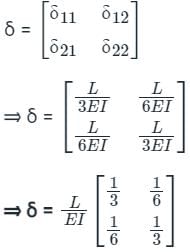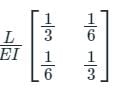Test: Matrix Method of Analysis - Civil Engineering (CE) MCQ
10 Questions MCQ Test - Test: Matrix Method of Analysis
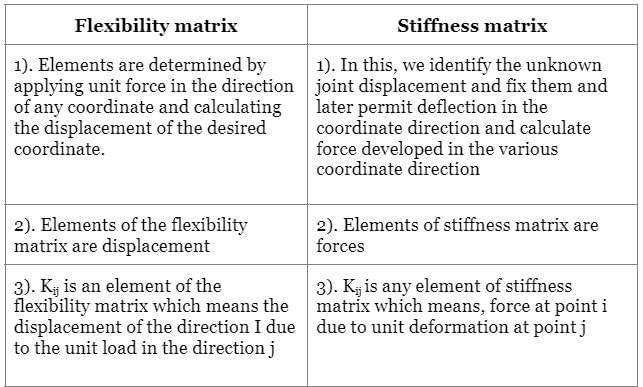
The stiffness matrix for a beam element is 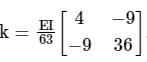 The corresponding flexibility matrix is
The corresponding flexibility matrix is
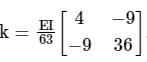 The corresponding flexibility matrix is
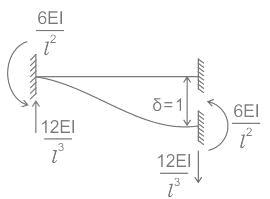
The corresponding flexibility matrix isStiffness matrix with reference to coordinates 1, 2 and 3 as shown in Fig. below is:
If the stiffness matrix of the beam element is given as 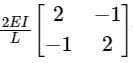 then the flexibility matrix is
then the flexibility matrix is
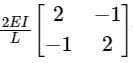 then the flexibility matrix is
then the flexibility matrix isTo generate the jth column of the flexibility matrix
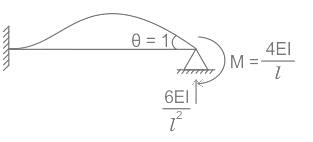
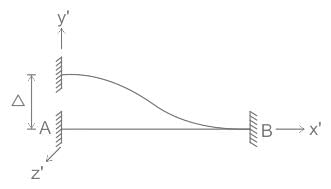
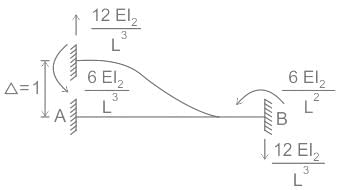
A stiffness matrix is to be generated for beam AB as a horizontal flexural member. As per the method adopted for calculation of stiffness matrix, if end A is given translational displacement in a vertically upward direction, the end forces generated at the end ‘B’ are
The stiffness matrix of a beam is given as 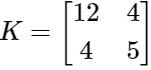 Calculate the flexibility matrix. Flexibility matrix will be ______.
Calculate the flexibility matrix. Flexibility matrix will be ______.
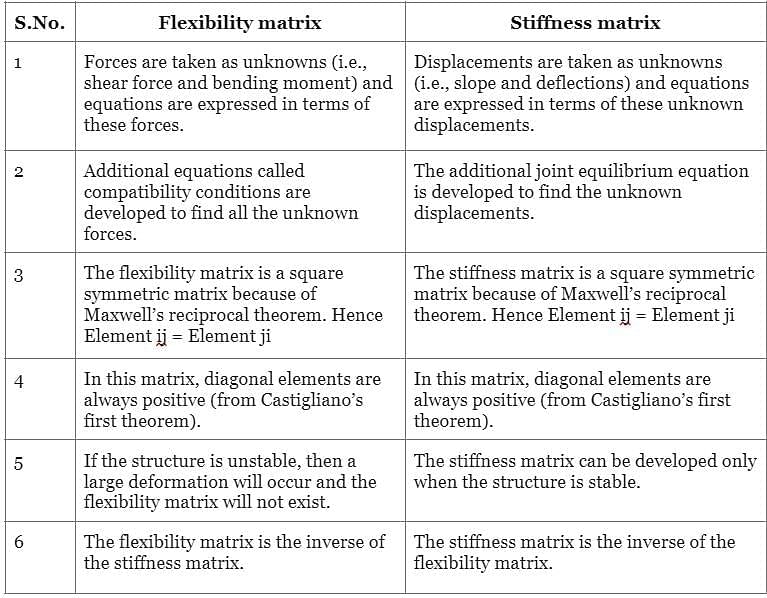
For stable structures, one of the important properties of flexibility and stiffness matrices is that the element on the main diagonal
(i) of a stiffness matrix must be negative.
(ii) of a stiffness matrix must be positive
(iii) of a flexibility matrix must be positive
(iv) of a flexibility matrix must be negative
In stiffness matrix method of structure analysis, the quantity taken as redundant is
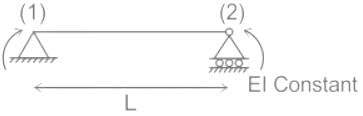
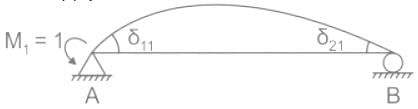
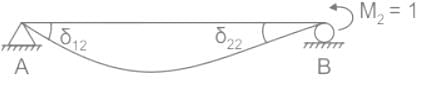
The flexibility matrix for the simply supported beam with reference to the coordinates, as shown below, is