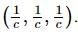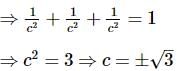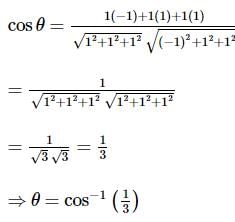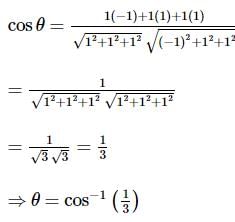BITSAT Mathematics Test - 5 - JEE MCQ
30 Questions MCQ Test - BITSAT Mathematics Test - 5
If cos 20° = k and cos x = 2k2-1, then the possible values of x between 0° and 360° are
The area enclosed between the curves y = x2 and x = y2 is
The differential coefficient of log (I log xl) with respect to log x is
Length of the tangent from (2,1) to the circle x2 + y2 + 4y + 3 = 0 is
If  then what is the standard deviation of all the terms?
then what is the standard deviation of all the terms?
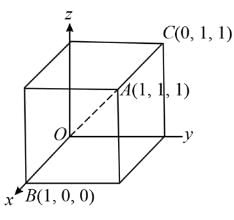
Consider the given three vectors:

If  are coplanar, then what is the value of
are coplanar, then what is the value of
A person is to select an onto function from all the functions F: A → A, where A = {2, 4, 6, 8, 10, 12, 14}. Find the probability of selecting onto function.
Consider the equations given below:
y = (1 - x)2
y = 0
x = 0
A straight line representing x = k separates the area enclosed by the above curves. Say both the areas are A1 (0 ≤ x ≤ k) and A2 (k ≤ x ≤ 1). If A1 - A2 = 1/4 , then what is the value of k?
Consider the function given below:
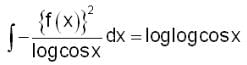
Which of the following statements is true?
Consider the given function:
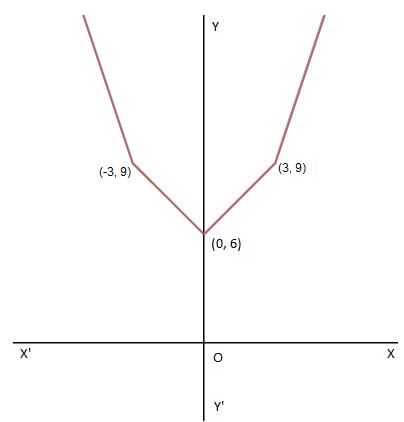
f(x) = |x - 3| + |x| + |x + 3|
The function is
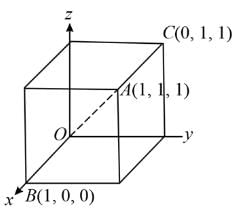
Points of intersection of a plane on the coordinate axes are P, Q and R. If (a, b, c) is the intersection point of the medians of ∆PQR, then what is the equation of the plane?
The total number of solutions of the system of equations 5x−y=3,y2−6x2=25 are
Let A(1,−1,2) A and B(2,3,−1) be two points. If a point P P divides AB AB internally in the ratio 2:3, then the position vector of P is


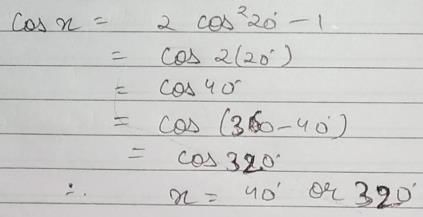

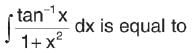
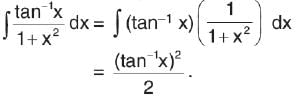
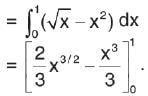
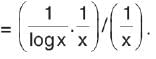
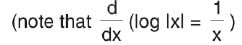
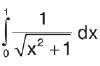 is equal to
is equal to 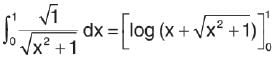
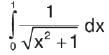 is equal to
is equal to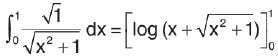
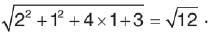



 are coplanar,
are coplanar,

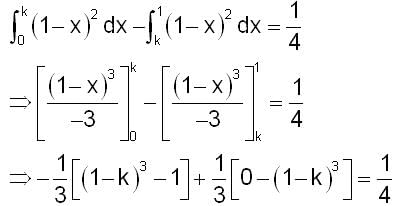
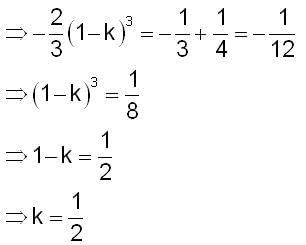
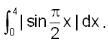
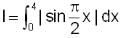
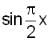 is positive when 0 < x < 2, and negative when 2< x < 4.
is positive when 0 < x < 2, and negative when 2< x < 4.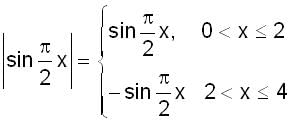
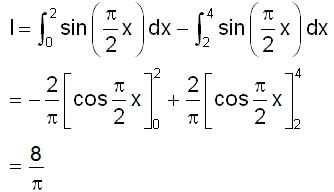
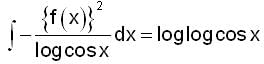
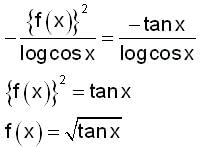
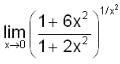
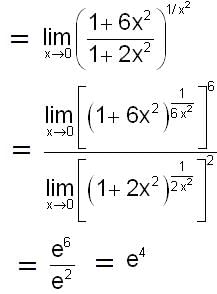
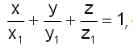 where x1, y1 and z1 are the intercepts made by the plane on the axes.
where x1, y1 and z1 are the intercepts made by the plane on the axes.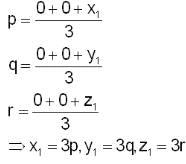
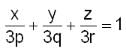
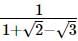 is equivalent to
is equivalent to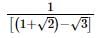
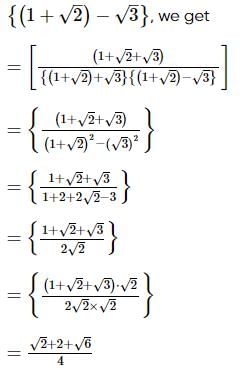
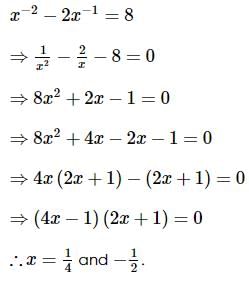
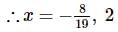
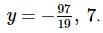
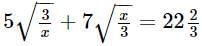 are
are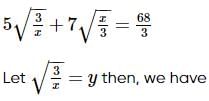
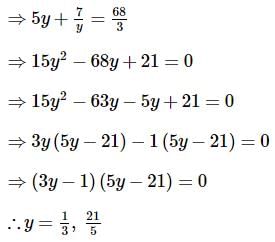
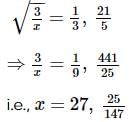
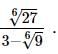
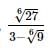
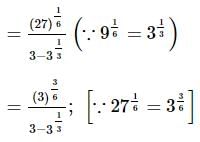
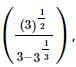 we will first obtain the rationalising factor of
we will first obtain the rationalising factor of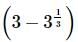
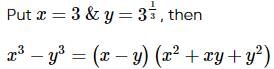
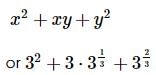
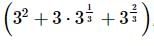 we get
we get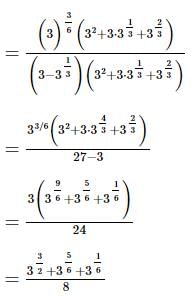
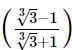 with rational denominator.
with rational denominator.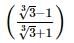
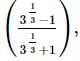 we will first obtain the rationalising factor of
we will first obtain the rationalising factor of 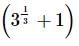
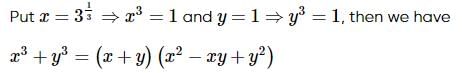
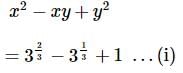
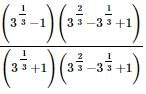
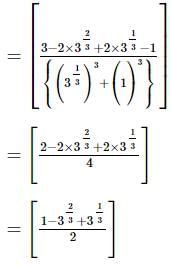

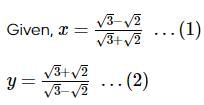
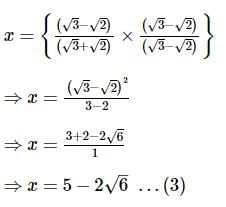
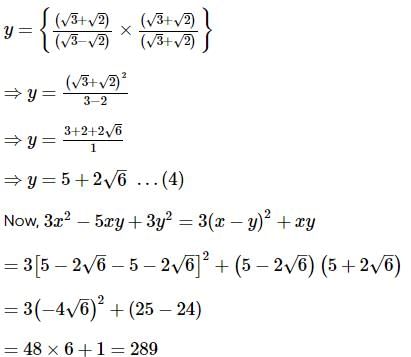
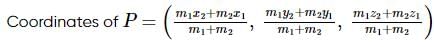
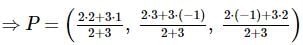
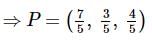
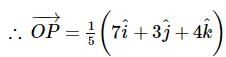
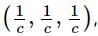 then
then