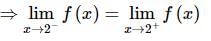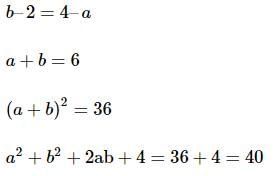BITSAT Mathematics Test - 9 - JEE MCQ
30 Questions MCQ Test - BITSAT Mathematics Test - 9
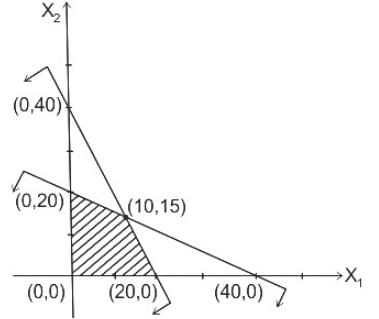
Consider the following LPP:
Maximize z = 60X1 + 50X2
Subject to X1 + 2X2 ≤ 40,
3X1 + 2X2 ≤ 60
where, X1 and X2 ≥ 0:
Maximize z = 60X1 + 50X2
Subject to X1 + 2X2 ≤ 40,
3X1 + 2X2 ≤ 60
where, X1 and X2 ≥ 0:
The solution of the differential equation  tan x = ex sec x is:
tan x = ex sec x is:
 tan x = ex sec x is:
tan x = ex sec x is:The volume of the tetrahedron included between the plane 3x + 4y - 5z - 60 = 0 and the coordinate planes is:
What is the equation of the straight line parallel to 3x + 2y + 1 = 0 and passing through the point (−1,−2)?
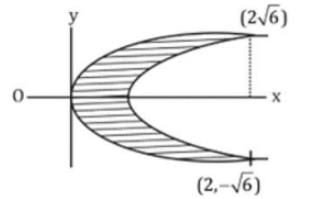
What is the area of the region bounded by the parabolas y2 = 6(x − 1) and y2 = 3x ?
Given that the events A and B are independent, if P(A′) = 2/3 and P(B′) = 2/7, then P(A∩B) is equal to:
The rate of change of volume of a sphere with respect to its surface area when the radius is 4 cm is:
If α is a root of x4 = 1 with negative principal argument, then principal argument of ω, where
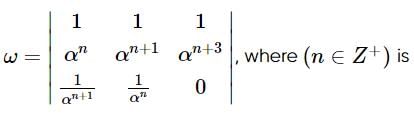
The shaded region, where P = (−1, 0), Q = (−1 + √2, √2), R = (−1 + √2,−√2), S = (1, 0) is represented by

If ω is an imaginary cube root of unity and x = a + b, y = aω + bω2, z = aω2 + bω, then x2 + y2 + z2 is equal t
The locus of a point P(z) which satisfies the equation |z + 3| + |z – 3| = 10 is (where z is a complex number)
In which quadrant of the complex plane, the point 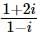 lies?
lies?
The equation zn − 1 = 0 and zm − 1 = 0 have only one common roots where m, n ∈ N then -
Let x = α + β, y = αω + βω2, z = αω2 + βω, ω is an imaginary cube root of unity. Product of xyz is
Let z1, z2 and z3 be the affixes of the vertices of a triangle having the circumcentre at the origin. If z is the affix of its orthocentre, then z is equal to
A function is defined as 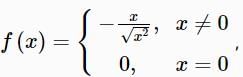 then which one of the following is correct in respect of the function?
then which one of the following is correct in respect of the function?
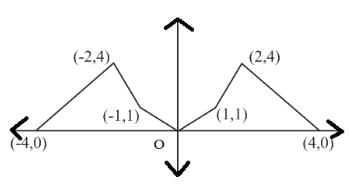
Let 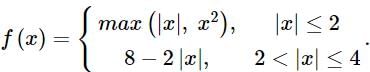 Let S be the set of points in the interval (−4, 4) at which f is not differentiable. Then S
Let S be the set of points in the interval (−4, 4) at which f is not differentiable. Then S
Let f : [−1, 3] → R be defined as
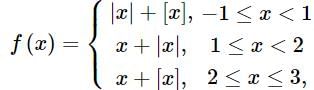
Where [t] denotes the greatest integer less than or equal to t. Then, f is discontinuous at:
Determine the value of f(0) so that f(x) is continuous at x = 0, if 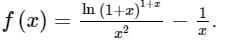
Number of points of discontinuity of f(x) = [sin−1x] − [x] in its domain is equal to (where [⋅] denotes the greatest integer function)
The function 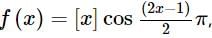 (where [.] denotes the greatest integer function) is continuous at
(where [.] denotes the greatest integer function) is continuous at
Let f(x) be the continuous function f : R → R satisfying f(0) = 1 and f(2x) − f(x) = x. Then the value of f(3) is:
A real function f is said to be continuous, if it is continuous at every point in the



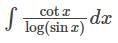
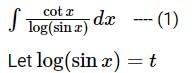
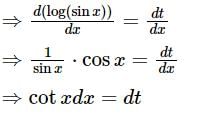
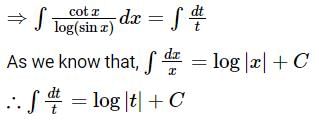
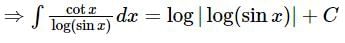

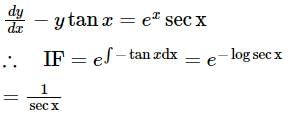
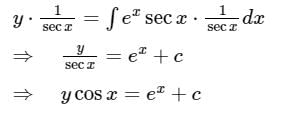
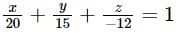
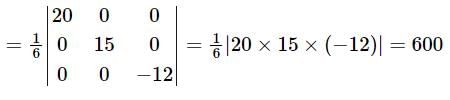
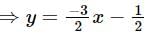
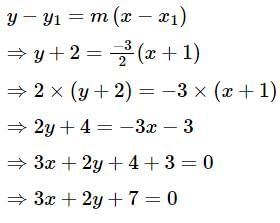

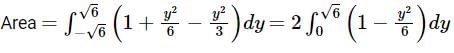
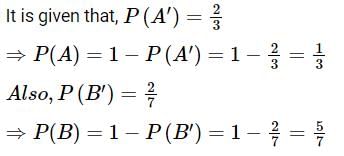
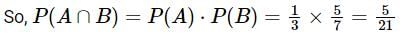

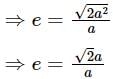
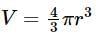
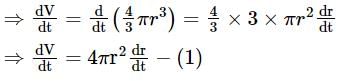
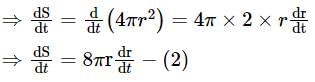
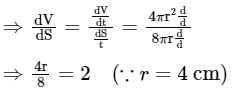
 is equal to?
is equal to?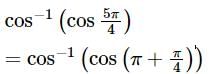
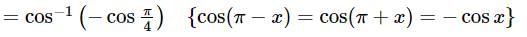
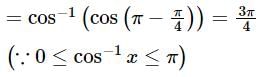
 common from R3
common from R3 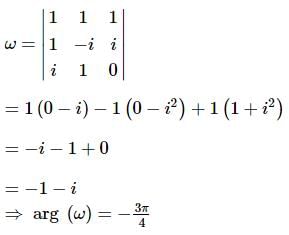
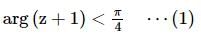
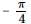
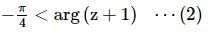
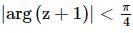
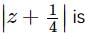
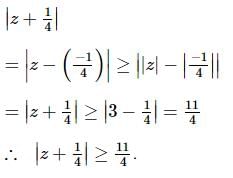
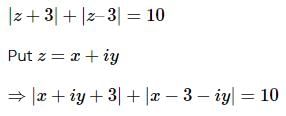
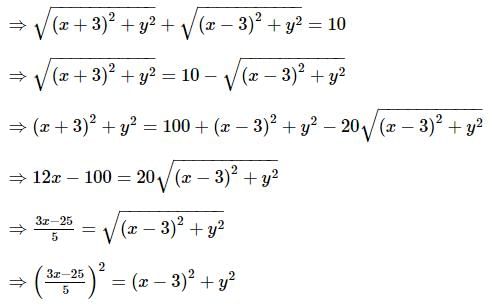
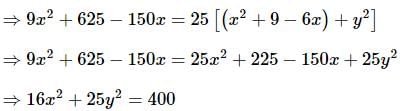
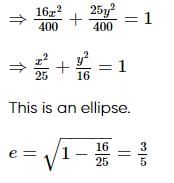
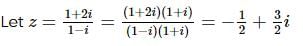
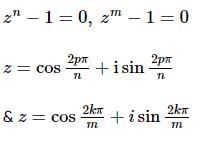
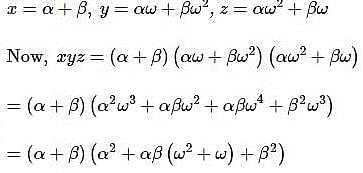
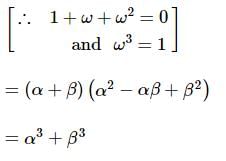
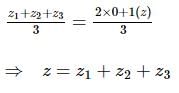

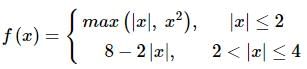

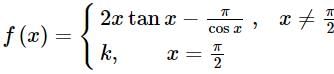 is continuous at x = π/2 then k =
is continuous at x = π/2 then k =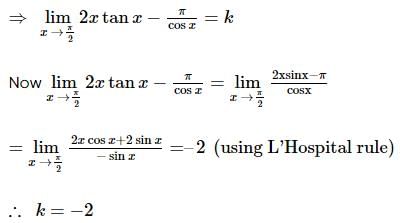

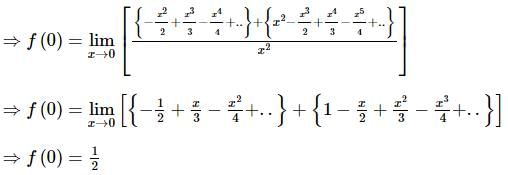
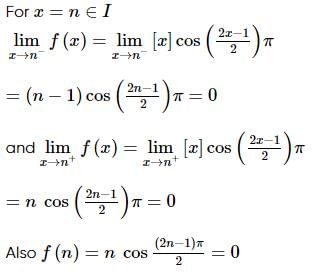
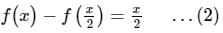
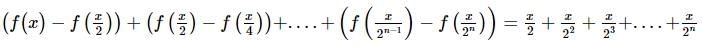
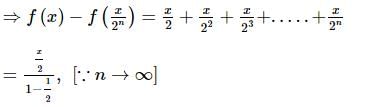
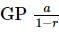 can be used.
can be used.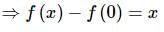
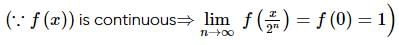

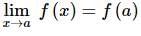
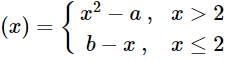 is continuous at x = 2, then a2 + b2 + 2ab + 4 is
is continuous at x = 2, then a2 + b2 + 2ab + 4 is