Test: Venn Diagram - Bank Exams MCQ
10 Questions MCQ Test - Test: Venn Diagram
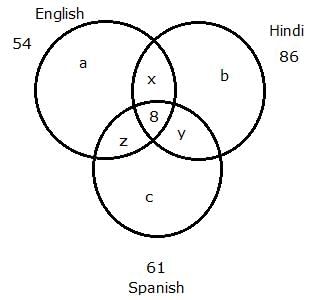
At a certain school, each of the 160 students takes atleast one of the 3 classes. The 3 classes available are English, Hindi and Spanish. 54 students study English, 86 study Hindi and 61 study Spanish. If 8 students take all 3 classes, how many take exactly 2 classes?
Instructions
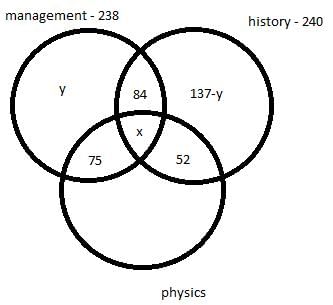
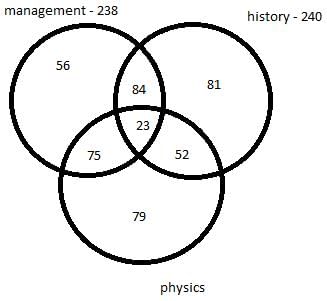
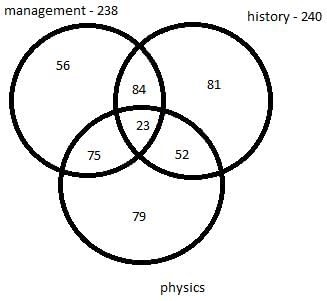
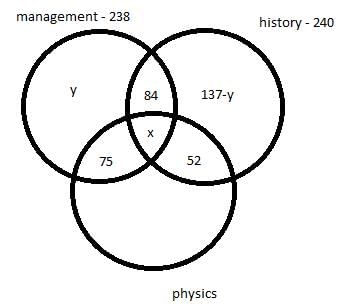
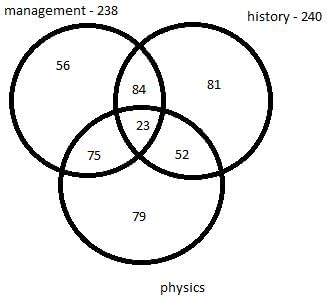
There are 450 students in a college. Each student has to choose one or more elective out of management, history and physics. Further following information is also known –
- 75 students selected only management and physics.
- 84 students selected only management and history.
- 52 students selected only physics and history.
- The number of students who selected only history is 137 less the number of students who selected only management.
- In total 238 students selected management as an elective.
- In total 240 students selected history as an elective.
Q. How many students selected both management and physics as elective?
Instructions
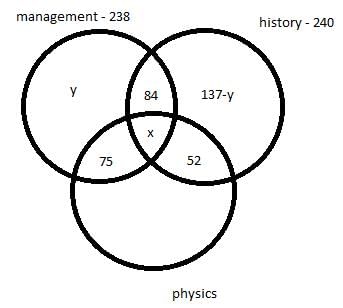
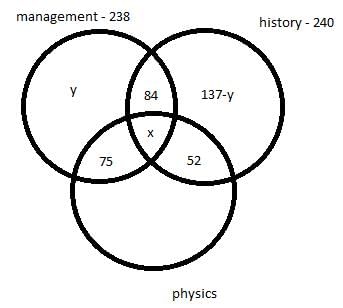
There are 450 students in a college. Each student has to choose one or more elective out of management, history and physics. Further following information is also known –
- 75 students selected only management and physics.
- 84 students selected only management and history.
- 52 students selected only physics and history.
- The number of students who selected only history is 137 less the number of students who selected only management.
- In total 238 students selected management as an elective.
- In total 240 students selected history as an elective.
Q. How many students selected the only history as an elective?
Instructions
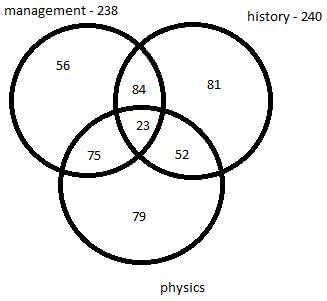
There are 450 students in a college. Each student has to choose one or more elective out of management, history and physics. Further following information is also known –
- 75 students selected only management and physics.
- 84 students selected only management and history.
- 52 students selected only physics and history.
- The number of students who selected only history is 137 less the number of students who selected only management.
- In total 238 students selected management as an elective.
- In total 240 students selected history as an elective.
Q. How many students selected only physics as an elective?
Instructions
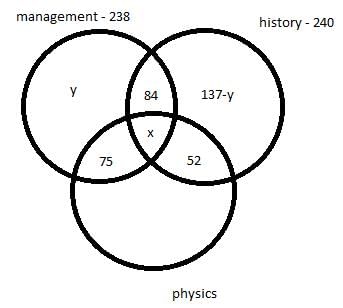
There are 450 students in a college. Each student has to choose one or more elective out of management, history and physics. Further following information is also known –
- 75 students selected only management and physics.
- 84 students selected only management and history.
- 52 students selected only physics and history.
- The number of students who selected only history is 137 less the number of students who selected only management.
- In total 238 students selected management as an elective.
- In total 240 students selected history as an elective.
Q. How many students selected only management as an elective?
Instructions
There are 450 students in a college. Each student has to choose one or more elective out of management, history and physics. Further following information is also known –
- 75 students selected only management and physics.
- 84 students selected only management and history.
- 52 students selected only physics and history.
- The number of students who selected only history is 137 less the number of students who selected only management.
- In total 238 students selected management as an elective.
- In total 240 students selected history as an elective.
Q. How many students select all the three electives?
In a locality consisting of 400 families, each family reads at least one newspaper. It is known that 200 families read ‘The Hindu’. 150 families read ‘Indian Express’ and 180 families read ‘Times of India’. If it is known that exactly 40 families read all three newspapers then how many families read exactly two newspapers?
Instructions
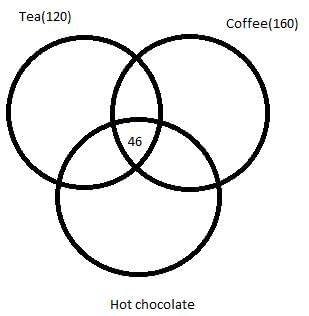
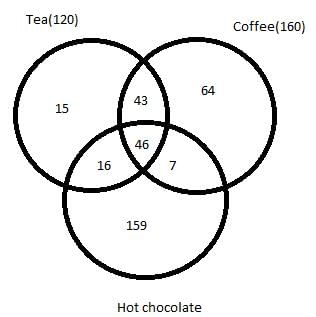
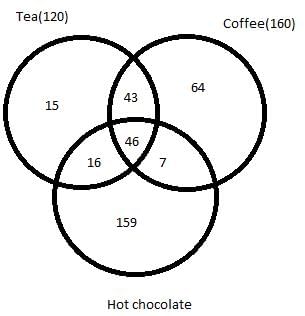
350 people are living in a particular village. There are three drinks Tea, Coffee and Hot chocolate available in the village. Each citizen has to vote for one or more of the three drinks which he/she like. It is known that:
- In total 120 people like Tea and 160 people like Coffee.
- 46 people like all the three drinks.
- 62 people like both Tea and Hot chocolate.
- 53 people like both Hot chocolate and Coffee.
- 89 people like both Tea and Coffee.
Q. How many people like only Tea?
Instructions
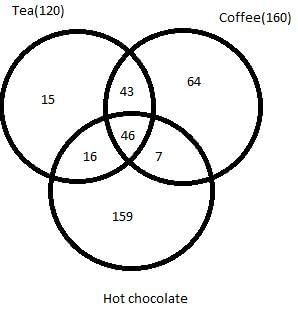
350 people are living in a particular village. There are three drinks Tea, Coffee and Hot chocolate available in the village. Each citizen has to vote for one or more of the three drinks which he/she like. It is known that:
- In total 120 people like Tea and 160 people like Coffee.
- 46 people like all the three drinks.
- 62 people like both Tea and Hot chocolate.
- 53 people like both Hot chocolate and Coffee.
- 89 people like both Tea and Coffee.
Q. How many people like only Coffee and Hot chocolate?
Instructions
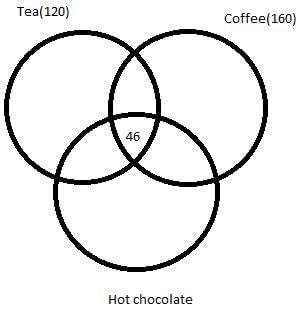
350 people are living in a particular village. There are three drinks Tea, Coffee and Hot chocolate available in the village. Each citizen has to vote for one or more of the three drinks which he/she like. It is known that:
- In total 120 people like Tea and 160 people like Coffee.
- 46 people like all the three drinks.
- 62 people like both Tea and Hot chocolate.
- 53 people like both Hot chocolate and Coffee.
- 89 people like both Tea and Coffee.
Q. How many people like only Hot chocolate?