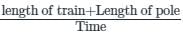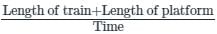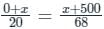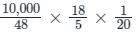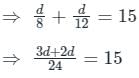Test: Speed, Time and Distance - 1 - UCAT MCQ
10 Questions MCQ Test - Test: Speed, Time and Distance - 1
A train has cross a pole in 20 seconds and 500 m long platform in 68 seconds. Find the speed of the train in km/hr.
A man travels 360 km in 4 h, partly by air and partly by train. If he had travelled all the way by air, he would have saved 4/5 of the time he travelled by train, and he would have arrived at his destination 2 h early. Find the distance he travelled by air.
A boat travels a certain distance upstream at 18 km/hr and the same distance downstream at 36 km/hr. Find the time the boat will take to travel 54 km upstream and downstream?
Two trains, one 152.5 m long and the other 157.5 m long, coming from opposite directions crossed each other in 9.3 seconds. The combined speed of the two trains every hour would then be:
A 1200 m long train crosses a tree in 120 sec, how much time will it take to pass a platform 700 m long?
A man leaves from P at 6 AM and reaches Q at 2 PM on the same day. Another man leaves Q at 8 AM and reaches P at 3 PM on the same day. At what time do they meet?
A person reaches his destination 32 minutes late if his speed is 6 km/h, and reaches 18 minutes before time if his speed is 7 km/h. Find twice the distance (in km) of his destination from his starting point.
A boat can travel 200 km upstream in 10 hours. If it increases its speed in still water by 10 km/hr, it can travel 140 km downstream in 2 hours. Find the speed (in km/hr) of the stream
Running at a speed of 60 km per hour, a train passed through a 1.5 km long tunnel in two minutes, What is the length of the train ?
A car travels some distance at a speed of 8 km/hr and returns at a speed of 12 km/hr. If the total time taken by the car is 15 hours, then what is the distance (in km)?