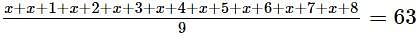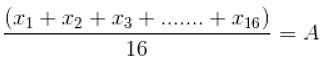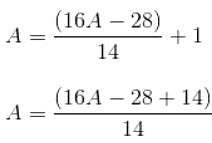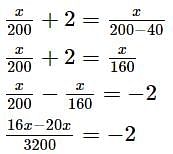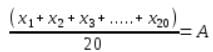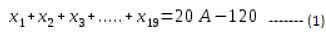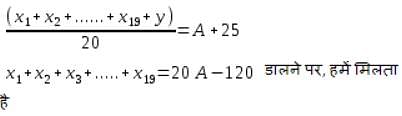Test: Average (औसत) - 2 - UPSC MCQ
20 Questions MCQ Test - Test: Average (औसत) - 2
मिलन, सोम और कृति की औसत ऊंचाई 156 सेमी है। यदि सोम और कृति की औसत ऊँचाई 140 सेमी और मिलन और सोम की औसत ऊँचाई 160 सेमी है, तो मिलन की ऊँचाई का कृति की ऊँचाई से अनुपात कितना है?
चार क्रमागत संख्याओं A, B, C और D का औसत 49.5 है। B और D का गुणनफल क्या है?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A, B एवं C के पास क्रमशः 40, x एवं y गेंदे है। यदि B,A को 20 गेंद देता है, तो B के पास गेंद की संख्या C की तुलना में आधी रह जाती है। यदि उनके पास 60 गेंद और अधिक होती, तो औसत 100 होता है। x एवं y का अनुपात है-
पहले 10 बक्सों में चॉकलेट की औसत संख्या 3,200 है, और अगले 12 बक्सों में 4,500 है। इन 22 बक्सों में कुल कितने चॉकलेट हैं?
सुशील ने हिंदी में 103 अंक, विज्ञान में 111 अंक, संस्कृत में 98 अंक, गणित में 110 अंक, और अंग्रेजी में 88 अंक प्राप्त किए। यदि प्रत्येक विषय के अधिकतम अंक बराबर हैं और सुशील द्वारा सभी विषयों में 85 प्रतिशत अंक प्राप्त किए जाते हैं, तो प्रत्येक विषय के अधिकतम अंक ज्ञात कीजिए।
10 लड़कों की औसत आयु 1.5 वर्ष बढ़ जाती है जब उनमें से एक की उम्र 16 वर्ष है, उसे एक नए लड़के द्वारा प्रतिस्थापित किया जाता है। नए लड़के की उम्र है:
अर्जुन के अनुसार, घंटाघर की ऊंचाई 46 मीटर से 54 मीटर के बीच है। देव के अनुसार, उसी घंटाघर की ऊंचाई 46 मीटर से 53 मीटर के बीच है। तुषार का विचार है कि उस घंटाघर की ऊंचाई 50 मीटर से कम है। यदि वे सभी अपने अनुमान में सही हैं, तो घंटाघर की विभिन्न संभावित ऊंचाइयों का औसत क्या है?
पाँच धनात्मक संख्याओं का औसत 308 है। प्रथम दो संख्याओं का औसत 482.5 है और अंतिम दो संख्याओं का औसत 258.5 है। तीसरी संख्या क्या है?
एक दुकानदार मार्च, अप्रैल, मई और जून के महीनों के लिए क्रमश: 48 रु/किलो, 46.50 रु/किलो, 52.50 रु/किलो और 54 रु/किलो में गेहूं खरीदता है । यदि दुकानदार प्रति माह 5000 रु खर्च करता है, तो प्रति किलो गेहूं की औसत लागत लगभग क्या है?
लगातार 5 संख्याओं की औसत संख्या n है यदि अगले दो संख्याओं को भी शामिल किया गया है, तो 7 संख्याओं की औसत संख्या क्या होगी?
13 मैचों के लिए एक खिलाड़ी का औसत स्कोर 42 रन है। यदि पहले 5 मैचों के लिए उसका औसत स्कोर 54 है, तब अंतिम 8 मैचों के लिए उसका औसत स्कोर (रनों में) क्या है?
सीता, गीता तथा रीटा की 8 वर्ष पहले औसत आयु 24 वर्ष थी | इसके साथ ही, सीता और रीटा की 5 वर्ष पहले औसत आयु 30 वर्ष थी | तीनों के वर्तमान आयु के योग में गीता की वर्तमान आयु का कितना भाग है?
एक संस्था के 120 सदस्यों की औसत आयु 60.7 वर्ष है। 30 नये सदस्यों के जोड़ने पर, औसत आयु 56.3 वर्ष हो जाती है। नये जुड़ने वाले सदस्यों की औसत आयु (वर्षों में) क्या है?
प्रश्न X, Y और Z जैसे तीन एसी के बारे में जानकारी देता है । X और Z का औसत क्रय मूल्य 48,000 रु है, X और Y का औसत क्रय मूल्य 54,000 रु है, और Y और Z का औसत क्रय मूल्य 44,000 रु है । X का वास्तविक क्रय मूल्य Y के वास्तविक क्रय मूल्य का कितना प्रतिशत है?
9 क्रमागत धनात्मक पूर्णांको का औसत 63 है। महत्तम और न्यूनतम पूर्णांकों का गुणनफल क्या है?
100 प्रेक्षणों का समांतर माध्य 24 हैं। उन प्रेक्षणों में प्रत्येक में 6 जोड़ने पर तत्पश्चात प्रत्येक को 2.5 से गुणा करने पर उनका नया समांतर माध्य कितना हो जाएगा?
16 छात्रों के समूह में, सबसे लंबे छात्र की आयु 16 वर्ष है और सबसे छोटे छात्र की आयु सबसे लंबे छात्र की आयु की (3/4) है। यदि सबसे लंबे और सबसे छोटे छात्रों की आयु को छोड़ दिया जाए, तो 14 छात्रों की औसत आयु, छात्रों की औसत आयु की तुलना में 1 वर्ष कम हो जाती है, जिसमें सबसे छोटे और सबसे लंबे छात्रों को शामिल नहीं किया जाता है। 16 छात्रों की औसत आयु क्या है?
बाल दिवस पर 200 बच्चों में मिठाइयां समान रूप से बांटी जानी थी। लेकिन उस दिन 40 बच्चे अनुपस्थित थे; इसलिए प्रत्येक बच्चे को 2 मिठाइयाँ अधिक मिलीं। कितनी मिठाइयां बांटी गई थी?
4 लगातार विषम संख्याओं का औसत 64 है तो सबसे बड़ी संख्या का मान क्या है?
एक बैग के अंदर 20 सेब हैं। जब 120 ग्राम वजन वाले बैग के अंदर सेब में से एक के स्थान पर एक और सेब आता है, तो औसत वजन 25 ग्राम बढ़ जाता है। उस सेब का वजन क्या है जो 120 ग्राम सेब का स्थान लेता है?


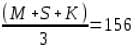
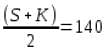
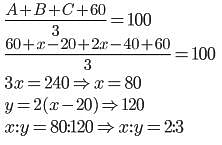

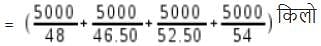
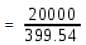 = 50.06 या रु. 50
= 50.06 या रु. 50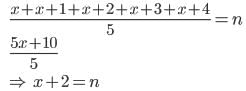
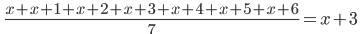
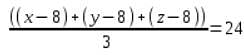
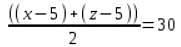
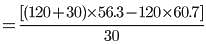
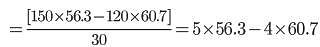
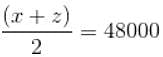
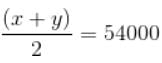
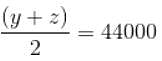
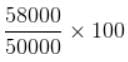 = 116%
= 116%