Test: Mixtures and Alligations (मिश्रण और आरोपण) - 1 - UPSC MCQ
10 Questions MCQ Test - Test: Mixtures and Alligations (मिश्रण और आरोपण) - 1
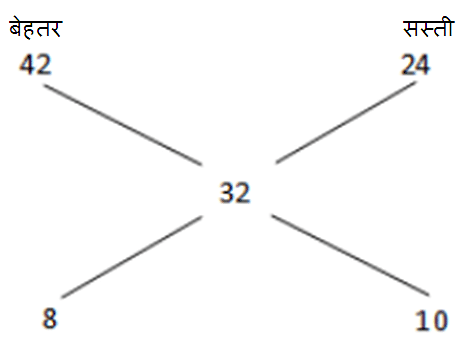
एक दुकानदार के पास चावल के दो किस्में हैं, बेहतर और सस्ता। चावल की बेहतर गुणवत्ता की कीमत रु. 42 प्रति किलो और सस्ती गुणवत्ता में रु. 24 प्रति किलो। चावल की सस्ती गुणवत्ता के लिए उसे 24 किलो चावल की बेहतर गुणवत्ता के साथ कितनी मात्रा में मिलाना चाहिए ताकि दुकानदार जब मिश्रण को रु.40 प्रति किलो की दर से बेचे, वह परिव्यय पर 25% हासिल करे?
समान क्षमता के दो बर्तनो में पानी और अल्कोहल हैं। पहला बर्तन, जिसमें अल्कोहल है, अपनी अधिकतम क्षमता तक भरा है, और दूसरा बर्तन, जिसमें पानी है, दो-तिहाई खाली है। पहले बर्तन की सामग्री को क्षमता के अनुसार भरने के लिए दूसरे बर्तन में डाला जाता है और फिर दूसरे बर्तन की सामग्री को पहले बर्तन में तब तक डाला जाता है जब तक वह भर न जाए, और फिर पहले बर्तन की सामग्री को पूरी तरह से भरने के लिए दूसरे बर्तन में डाला जाता है। यदि हम ऑपरेशन को चौथी बार दोहराते हैं जैसे कि पहले पात्र को दूसरे पात्र की सामग्री डालकर आधा भरा जाता है, तो पहले पात्र पानी - अल्कोहल का अनुपात क्या होगा?
एक पात्र में दो तरल पदार्थ A और B का मिश्रण 80 लीटर है। जब कुल मिश्रण का 55% निकाला गया, तो यह पाया गया कि निकाले गए मिश्रण में 70% तरल A और 30% तरल B थे। पात्र में तरल A और तरल B की प्रारंभिक मात्रा क्या थी?
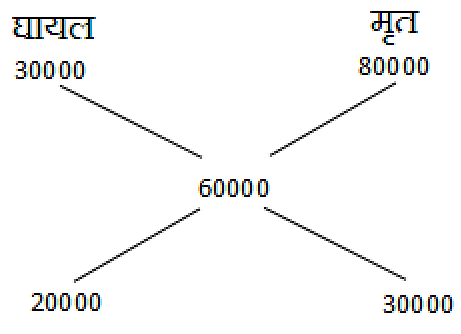
39,00,000 रुपये की राशि ट्रेन दुर्घटना के पीड़ितों को मुआवजा प्रदान करने के लिए आवंटित की गयी हैं। अधिकारियों ने घायलों को 30,000 रुपये और मृत यात्रियों के परिवारों को 80,000 रूपये की राशि को मंजूरी देने का फैसला किया है। यदि कुल 65 पीड़ित हैं, तो घायल यात्रियों की संख्या का पता लगाएं।
एक दूधवाला न तो लाभ न ही हानि पर 25 रु प्रति लीटर में दूध बेच रहा है । वह अनुपात निर्धारित करें जिसमें उसे दूध के साथ पानी मिलाना चाहिए ताकि इसे 20 रु प्रति लीटर पर बेचने पर, वह 25% का लाभ कमा सके ।
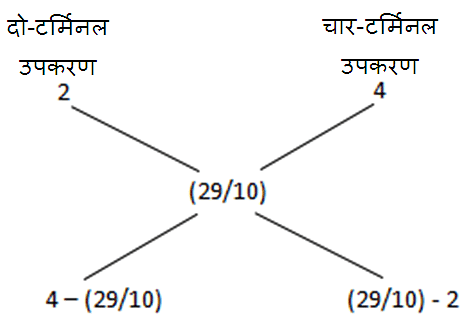
अर्धचालक उपकरण, कुछ दो टर्मिनलों के साथ और कुछ चार टर्मिनलों के साथ, एक टेबल पर रखे हैं। जब गिना जाता है, तो कुल 580 टर्मिनल और 200 उपकरण होते हैं। टेबल पर कितने दो-टर्मिनल उपकरण हैं?
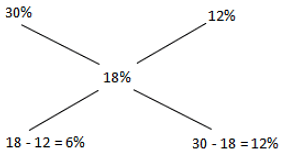
एक सुराही में शराब और पानी का मिश्रण होता था। इसमें 30% शराब और बाकी पानी था। एक व्यक्ति ने मिश्रण के कुछ हिस्से को हटा दिया और इसे दूसरे शराब-पानी के मिश्रण से बदल दिया, जिसमें शराब केवल 12% थी। नया मिश्रण तब 18% वाइन और बाकी पानी से युक्त पाया गया था। शराब-पानी के मिश्रण का क्या हिस्सा बदला गया था?
मिश्रण A और B दो अलग-अलग बर्तनों में निहित हैं। मिश्रण A में, 3 : 5 : 2 के अनुपात में P, Q और R सामग्री शामिल है और मिश्रण B में 4 : 5 के अनुपात में P और Q सामग्री शामिल है। हमें 1 : 2 के अनुपात में A और B को जोड़कर 540 लीटर नया मिश्रण बनाना है, तो अंतिम मिश्रण में सामग्री P की मात्रा क्या होगी?
एक कंटेनर चीनी की चाशनी से भरा है। 4 गैलन चाशनी को कंटेनर से निकाला जाता है और पानी से बदल दिया जाता है। इस पानी-चाशनी मिश्रण से, 4 गैलन मिश्रण को फिर से निकाला जाता है और पानी से बदल दिया जाता है। कंटेनर में पानी के लिए चीनी की चाशनी का अनुपात 36 : 13 पाया गया था। कंटेनर में कितने गैलन है?
तांबे और ज़िंक के एक मिश्रित नमूने में 5% तांबा है और शेष ज़िंक है। यदि यह ज्ञात है कि नमूने का वजन 180 किलोग्राम है, तो मिश्र धातु में कितना तांबा मिलाया जाना चाहिए, ताकि मिश्र धातु में तांबा की मात्रा 10% हो जाए?


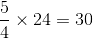 किलोग्राम
किलोग्राम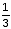 W +
W + 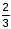 A
A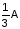 +
+ 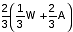
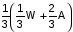
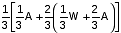
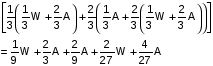
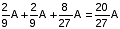
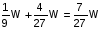
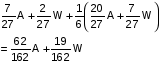

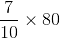 = 56 लीटर
= 56 लीटर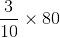 = 24 लीटर
= 24 लीटर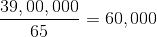
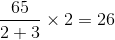
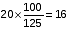 प्रति लीटर
प्रति लीटर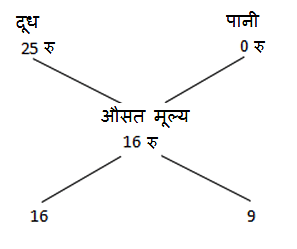
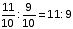
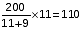
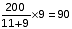
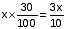 लीटरमिश्रण में प्रतिस्थापित शराब की मात्रा =
लीटरमिश्रण में प्रतिस्थापित शराब की मात्रा = 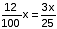 लीटर
लीटर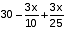 लीटर
लीटर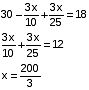
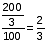
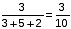 लीटर
लीटर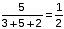 लीटर
लीटर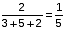 लीटर
लीटर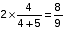 लीटर
लीटर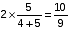 लीटर
लीटर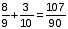
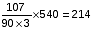 लीटर
लीटर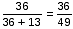 कंटेनर की कुल मात्रा का
कंटेनर की कुल मात्रा का














