XAT Quantitative Ability And DI MCQ Quiz - 2 - CAT MCQ
29 Questions MCQ Test - XAT Quantitative Ability And DI MCQ Quiz - 2
There are five identical green dyes, four identical blue dyes, three identical yellow dyes and four different red dyes. How many combinations of dyes can be chosen taking at least one green, at least one blue and at least one red dye?
Three friends - Annie, Bobby and Carole like to play with numbers. Annie picks a random natural number x, triples it and gives the result to Bobby. Each time Bobby gets a number from Annie; he adds 75 to the number and gives the result to Carole. Each time Carole gets a number from Bobby, she doubles the number and subtracts 50 from it and gives the result to Annie. Annie again triples it and gives the result to Bobby and this process continues. The first person to receive a 5-digit number (from other) is declared the winner. If Bobby wins the game, what is remainder when the least possible value of x is divided by 13?
Group Question
Answer the following question based on the information given below.
Rakesh, Rajesh, Rupesh, Paresh and Suresh were hired by Glotel information as sales officers to sell simcards on a contract basis. For each simcard sold on day 1 and day 2, each sales officer was given Rs. 25; and an amount of Rs. 5 was deducted for each unsold simcard from the amount they had earned in the day. On the 1st day, each sales officer was given 25 simcards to sell.
On the 2nd day, each sales officer was allowed to sell any number of simcards from Glotel information at the cost of Rs. 5 per simcard, from the money earned on day 1.
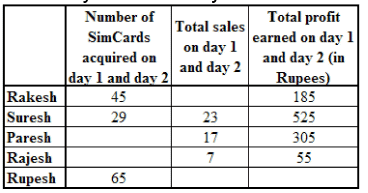
Q. How many simcards did Rajesh sell on day 1?
Rakesh, Rajesh, Rupesh, Paresh and Suresh were hired by Glotel information as sales officers to sell simcards on a contract basis. For each simcard sold on day 1 and day 2, each sales officer was given Rs. 25; and an amount of Rs. 5 was deducted for each unsold simcard from the amount they had earned in the day. On the 1st day, each sales officer was given 25 simcards to sell.
On the 2nd day, each sales officer was allowed to sell any number of simcards from Glotel information at the cost of Rs. 5 per simcard, from the money earned on day 1.
Rakesh, Rajesh, Rupesh, Paresh and Suresh were hired by Glotel information as sales officers to sell simcards on a contract basis. For each simcard sold on day 1 and day 2, each sales officer was given Rs. 25; and an amount of Rs. 5 was deducted for each unsold simcard from the amount they had earned in the day. On the 1st day, each sales officer was given 25 simcards to sell.
On the 2nd day, each sales officer was allowed to sell any number of simcards from Glotel information at the cost of Rs. 5 per simcard, from the money earned on day 1.
Q. Which of the following may not be the profit for Rakesh on day 1?
Rakesh, Rajesh, Rupesh, Paresh and Suresh were hired by Glotel information as sales officers to sell simcards on a contract basis. For each simcard sold on day 1 and day 2, each sales officer was given Rs. 25; and an amount of Rs. 5 was deducted for each unsold simcard from the amount they had earned in the day. On the 1st day, each sales officer was given 25 simcards to sell.
On the 2nd day, each sales officer was allowed to sell any number of simcards from Glotel information at the cost of Rs. 5 per simcard, from the money earned on day 1.
Q. What is the total number of simcards acquired by all 5 sales 0fficers to sell on day 1 and day 2?
Rakesh, Rajesh, Rupesh, Paresh and Suresh were hired by Glotel information as sales officers to sell simcards on a contract basis. For each simcard sold on day 1 and day 2, each sales officer was given Rs. 25; and an amount of Rs. 5 was deducted for each unsold simcard from the amount they had earned in the day. On the 1st day, each sales officer was given 25 simcards to sell.
On the 2nd day, each sales officer was allowed to sell any number of simcards from Glotel information at the cost of Rs. 5 per simcard, from the money earned on day 1.
Q. If the total profit for Rupesh was the highest among the 5 sales officers, then what is the minimum number of simcards sold by Rupesh on day 1 and day 2?
Rakesh, Rajesh, Rupesh, Paresh and Suresh were hired by Glotel information as sales officers to sell simcards on a contract basis. For each simcard sold on day 1 and day 2, each sales officer was given Rs. 25; and an amount of Rs. 5 was deducted for each unsold simcard from the amount they had earned in the day. On the 1st day, each sales officer was given 25 simcards to sell.
On the 2nd day, each sales officer was allowed to sell any number of simcards from Glotel information at the cost of Rs. 5 per simcard, from the money earned on day 1.
Q. If Paresh sold 12 simcards on day 1, then what is the difference between the number of unsold simcards on day 1 and day 2 for Paresh?
Group Question
Answer the following question based on the information given below.
Andy buys four articles, A, B, C, D for a sum of Rs x. He uses A and sells the rest to Bob for Rs. x. Bob uses B and sells the rest to Charlie for Rs. x. Charlie uses C and sells D to David for Rs.x. It is known that Andy, Bob and Charlie made a profit of 20%, 25% and 50% respectively. Also x = 100.
Q. How much did Charlie earn?
Andy buys four articles, A, B, C, D for a sum of Rs x. He uses A and sells the rest to Bob for Rs. x. Bob uses B and sells the rest to Charlie for Rs. x. Charlie uses C and sells D to David for Rs.x. It is known that Andy, Bob and Charlie made a profit of 20%, 25% and 50% respectively. Also x = 100.
Q. For how much more than Andy did Bob buy B, C and D?
Ajay and Suresh are playing a game of dice. Suresh, being the evil one, loaded the dice in such a way that the probability of getting any number n is n times the probability of showing up of 1 when the dice is rolled. The rules of the games are such that for every time an odd number shows up, Ajay scores a point, otherwise the point goes to Suresh. What is the probability of Ajay scoring a point at any single roll?
Given that k = 2 - (|x - 2| + |x + 2.4|). Find the number of integral values of x for which k takes the maximum possible value.
Baban Narang, a shooting expert, once decides to practice his shooting skills by targetting a wall clock. His bullet takes 10 seconds to travel to the clock after leavng his rifle. Just before he fires the bullet, the clock shows 5:30:00 pm. What is the probability that the bullet strikes in the smaller angle made between the minute hand and the second hand? Assume that the bullet definitely hits the clock with all points on the clock being equally likely targets.
Group Question
Answer the following question based on the information given below.
The following graphs give annual data of the net income, profit (as percentage of net income) and bonus provided to the employees (as percentage of the profit) of a company during the period 2006 - 2010.
Q. The company has 1000 employees in the year 2008 and 1200 employees in the year 2010. By what approximate percentage did the average bonus received by each employee increase in 2010 over 2008?
The following graphs give annual data of the net income, profit (as percentage of net income) and bonus provided to the employees (as percentage of the profit) of a company during the period 2006 - 2010.
Q. What is the approximate percentage of the total net income that was given away as bonus by the company during the period 2006 to 2010?
The following graphs give annual data of the net income, profit (as percentage of net income) and bonus provided to the employees (as percentage of the profit) of a company during the period 2006 - 2010.
Q. If the average bonus received by each employee remained constant in the years 2006 and 2007, then by what percentage did the number of employees increase in 2007 as compared to that in 2006?
The following graphs give annual data of the net income, profit (as percentage of net income) and bonus provided to the employees (as percentage of the profit) of a company during the period 2006 - 2010.
Q. The net income of the company increases by 25% in 2011 as compared to that in 2010, and each of the 1000 employees receives the bonus of Rs. 4500 in 2011. What is the percentage increase in the amount of profit earned by the company in 2011 as compared to that in 2010, if it is given that the company had distributed 15% of the profit earned in 2011 as bonus?
Each question is followed by two statements, A and B. Choose the most appropriate options given below.
In trapezium ABCD, AB || CD, and AB = 2 and BC = 8. Angle bisector ADC meets BC in E. What is the area of trapezium ABCD?
A. E is the midpoint of BC.
B. AD = 10
The teacher asked a class of fifth grade students to find the average of 15 different two-digit numbers displayed on the blackboard. After the students finished the exercise, the teacher wrote the correct answer on the blackboard. Ankit, in an attempt to impress the teacher, claimed that he could reverse the digits of one of the numbers so that the new number also was a two-digit number, and the average he would get would be 2.4 more than the result displayed.
What is the probability of Ankit finding such a number on the blackboard?
What is the sum of all roots of f(x)?
There is a set, A of six whole numbers having mean 16. Few facts about the numbers of A are: 12 is the only mode and the median is 15. What is the minimum possible value of the largest number from this set?
Group Question
Answer the following question based on the information given below.
The graph below shows the total domestic sales of three detergent brands (in Rs. crores) over a period of six years.
Q. Over the entire period, what is the maximum average annual growth rate achieved by any of these three brands?
The graph below shows the total domestic sales of three detergent brands (in Rs. crores) over a period of six years.
Q. For any detergent brand in country X, if the exports (in Rs. crores) in a particular year do not exceed the domestic sales for that year, which of these statement(s) is/are definitely true?
I. The exports of Surf can exceed the average domestic sales of Ariel in at most two years.
II. The exports of Nirma in 2010 are more than the total exports of Ariel in 2005 and 2006.
III. The exports of Surf in 2007 cannot be equal to the maximum value of its exports in 2008.
The graph below shows the total domestic sales of three detergent brands (in Rs. crores) over a period of six years.
Q. An analyst working on these figures erronously applied the growth rate of Surf from 2008 to 2009 to Ariel for the same period. However, he applied the correct growth rates every where else. What value did he get (in Rs. crores) for domestic sales of Ariel in 2010?
Each question is followed by two statements, A and B. Choose the most appropriate options given below.
Roots of x3 + ax2 + bx + c = 0 are integers and are in arithmetic progression. If a, b, and c are also integers, then what is the value of a + b + c?
A. a2 = 3(b + 4) and 4a < b < 6a
B. 5a = b + 4 and c = 7a
There are 6 straight lines in a plane, no two of which are parallel and no three of which pass through the same point. If their points of intersection are joined, then the number of additional lines thus introduced is:
A regular hexagon is inscribed in a circle of radius 7 cm. Inside the hexagon a rectangle is inscribed such that it touches the hexagon at the midpoints of its sides. A circle, whose centre coincides with that of the outer circle, is inscribed in the rectangle and an equilateral triangle is inscribed in the smaller circle. What is the length of the side of the triangle?
Which condition should hold true if the equation
has real roots that are equal in magnitude but opposite in sign?
If (1 - 2x) * log (2.5m) = (x - 1) * log m, then which of the following best describes x?



















