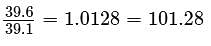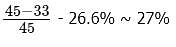Test: Quantitative Reasoning (Level 600) - 2 - GMAT MCQ
21 Questions MCQ Test - Test: Quantitative Reasoning (Level 600) - 2
How many integers will satisfy the inequality x+4 > |x+10| ?
The average of 13 numbers is 68. The average of the first 7 numbers is 63, and the average of the last 7 numbers is 70. What is 7th the number?
Juan and his five friends will sit on six fixed seats around a circular table. If Juan must sit on the seat closest to the window and Jamal must sit next to Juan, in how many can Juan and his five friends sit?
Tammy bikes the course of a race at 30 miles per hour, then returns home along the same route at 10 miles per hour. If the total time it takes her to travel the course and return home is 2 hours, and if the time spent turning around is negligible, what is the length, in miles, of the race course?
If <n> is the greatest integer less than or equal to n, what is the value of (<-2.1>)*(<2.1>)*(<2.9>) ?
If a and b are non-zero integers and ab >b, which of the following must be true?
I. a/b > 0
II. (a - b) > 0
II. (a + b) > 1
If a, b, c are non zero integers and a > bc, then which of the following must be true :
I. a/b > c
II. a/c > b
III. a/bc > 1
What is the least value of n for which the product of the first n positive integers is divisible by 405?
Ben is stocking milk at the local JumboMart. The milk cooler holds 780 cartons of milk and is completely full when Ben starts his shift. The store sells 75 percent of the milk during the first hour that Ben works and then sells another 20 percent of the remaining milk during the second hour. If there are 1000 cartons of milk in the back room, how many of them will Ben not need in order to restock the milk cooler?
When positive integer y is divided by 7, the remainder is 2. When y is divided by 11, the remainder is 3. What is the sum of the digits of the smallest possible value that meets the definition for y?
A certain roller coaster ride has between 29 and 150 people waiting in line to board. If riders are let on only in groups of 5 there will be 2 riders that do not get on. If the riders are let on only in groups of 6 all riders will be able to get on. Which of the following is the sum of the greatest possible number of people in the line and the least possible number of people in the line?
If the square of the 7th term of an arithmetic progression with positive common difference equals the product of the 3rd and 17th terms, then the ratio of the first term to the common difference is:
A certain purse contains 30 coins, Each coin is either a nickel or a quarter. If the total value of all coins in the purse is 4.70$, how many nickels does the purse contain?The value of each nickel is $0.05,
In three years, Janice will be three times as old as her daughter. Six years ago, her age was her daughter’s age squared. How old is Janice?
Working alone at its constant rate, Machine A can produce 1,050 electrical components in 5 hours. Machine B, working alone, can produce 1,050 electrical components in 15/2 hours. If the two machine work simultaneously for T hours and produce 1,050 electrical components, how many electrical components has Machine B produced at the end of T hours?
Working alone Jerry can complete a work in 6 minutes. Working alone, Adam can complete a work in 8 minutes. Working together, Jerry leaves the work after 2 minutes. How long will it take Adam to complete the work?
Four female friends & four male friends will be pictured in a advertising photo. If the photographer wants to line them up in one row, with men & women alternating. How many possible arrangements may she chose?
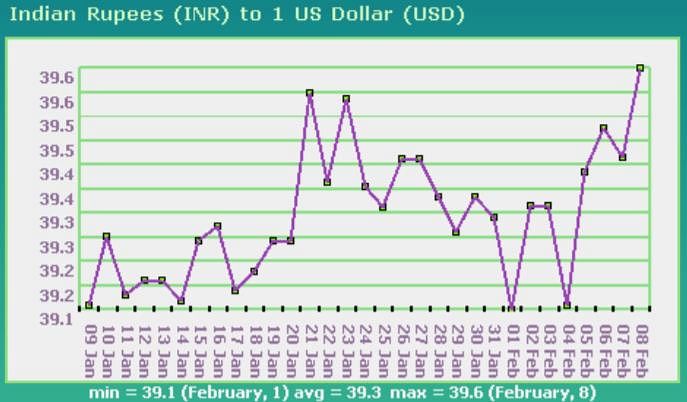
On February 8, the dollar value was approximately what percent of the dollar value on January 9?
For the age-group 50 and older, the number of people who indicated the Internet as their preferred method to obtain news is approximately what percent less than the number of people who indicated radio?

In what ratio should a mixture of milk and water in the ratio of 3:4 be mixed with another mixture of milk and water in the ratio 5:2 so that the resultant mixture contains equal quantities of milk and water?
Ben has 30 pencils in a box. Each of the pencils is one of 5 different colors, and there are 6 pencils of each color. If Ben selects pencils one at a time from the box without being able to see the pencils, what is the minimum number of pencils that he must select in order to ensure that he selects at least 2 pencils of each color?