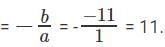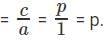Test: Absolute Equations- 2 - Telangana Police Constable MCQ
25 Questions MCQ Test - Test: Absolute Equations- 2
If x2 < 25, which of the following expressions must be true?
I.|x-3| < 10
II.|2x – 3| < 8
III. |2x2| < 42
If p and q are two integers on the number line such that q is on the right hand side of 0 and p is on the right hand side of q at a distance from q that is three times the distance between 0 and q, then what is the least possible distance on the number line between the number -16 and the product of p and q?
Seven water stations were set up at regular intervals along the 42-kilometer route of a marathon, with the last water station at the finish point. If James maintained a uniform running speed throughout the marathon, did not turn back at any time and reached the finish line, in how much time did he run the marathon?
(1) 40 minutes after the start of the marathon, James was 4 kilometers away from the second water station
(2) 20 minutes before reaching the finish point, James was 20 kilometers away from the third water station
If x and y are non-zero numbers and the value of is -1, which of the following expressions must be true?
While driving in one direction on a straight highway, James moves past three inns - Bethlem Inn, The Antimone and The Soliloquy, not necessarily in that order, and then stops at Stoby’s Restaurant for lunch. If the distance between Bethlem Inn and Stoby’s Restaurant is 90 kilometres, what is the distance between The Antimone and Stoby’s Restaurant?
(1) The distance between Bethlem Inn and The Soliloquy is 50 kilometres
(2) The distance between The Antimone and The Soliloquy is 40 kilometres
A shopkeeper purchased two TV sets A and B at the same price. If he sold the sets A and B at price P and Q respectively, such that |P-Q| = 20% of P, on which TV set did he make a greater profit?
(1) Set A was sold at no discount, while set B was sold at a discount of 25 percent
(2) The shopkeeper made a profit of 25 percent on set A
If y = |x-2| + |x| - |x+2| where x is an integer, then y can take how many non-zero integral values between -10 and 10, exclusive?
What is the remainder when the positive integer x is divided by 5?
(1) |x- 5y| = 3, where y is a positive integer
(2) |x| + 2 is divisible by 15
If x is a non-zero integer, is x prime?
(1) The number x is at a distance less than 2 units from the number 1.5 on the number line.
(2) The sum and product of roots of a quadratic equation ax2+bx+c are 5 and 6 respectively.
If integers p and q are the roots of the equation ax2 + bx + c = 0, where a, b and c are constants and a > 0, by what percentage is c greater than |b|?
(1) |p+1| = |q – 3|
(2) The greatest number that divides both |p| and |q| is 2 and the smallest number that is divisible by both |p| and |q| is 12
If |x - 5| = 2|x - 8|, then what is the value of x?
(1) |x2 – 100| > 50
(2) |x2 – 49| =0
|x + 3| = |y -4|, where x and y are non-zero integers. If |x| < 5 and |y| < 5, what is the maximum possible value of -|xy|?
If |x + 4| = 8, what is the sum of all the possible values of x?
On the number line shown, the distance between 0 and a, a and b and a and c is in the ratio of 1:2:3. If the distance of point b from 15 is twice the distance of point a from 15, what is the value of |c|?
What is the value of integer x?
(1) x + x2 = 0
(2) |x| + x2 = 2x
The positive integer y is at a distance of 2 units from the nearest multiple of a single digit positive integer x. What is the minimum positive value that should be added to y, so that it becomes divisible by x?
(1) y is x/2 units more than the square of x, where x/2 is even
(2) y – 3 is a multiple of 5
If x is an integer, is x2 > 25?
(1) |x – 3| > 5
(2) (x + y)2 > 49, where y is an integer such that |y| < 2
If z is an integer such that ||z - 30| - 43| = 62 which of the following could be value of |r|, where r is the remainder obtained when z is divided by 7?
I. 0
II. 2
III. 4
List A = {-x, x, |x|, x2, -6, 6}
If x is a non-zero integer such that -5 ≤ x ≤ 5, the ratio of the range of the list A to the median of the list A must lie between which of the following?
If P & Q are integers such that |P|Q=4 , is P negative?
(1) |P|+|Q|=|P+Q|
(2) P2−5|P|+4=0
If m is a negative integer and , then n can take how many positive values?
If x > 0, how many integer values of (x, y) will satisfy the equation 5x + 4|y| = 55?
If p > 0, and x2 - 11x + p = 0 has integer roots, how many integer values can 'p' take?
How many real solutions exist for the equation x2 – 11|x| - 60 = 0?
If the curve described by the equation y = x2 + bx + c cuts the x-axis at -4 and y axis at 4, at which other point does it cut the x-axis?