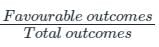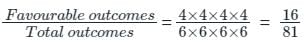MCQ Test: Axiomatic Probability - Bank Exams MCQ
10 Questions MCQ Test - MCQ Test: Axiomatic Probability
A box contains six red balls and four green balls. Four balls are selected at random from the box. What is the probability that two of the selected balls will be red and two will be green?
A bag contains 3 white, 2 blue and 5 red balls. One ball is drawn at random from the bag. What is the probability that the ball drawn is not red?
In a competition two persons, A and B wrote an exam. The probability of A's pass is 3/7 and the probability of B's pass is 3/5. What is the probability that only one of them is passed out?
A box contains 25 balls of two colours, red and white. If the probability of picking a red ball at random is 2/5, what is the probability of picking first ball red and second ball white without replacement?
An unbiased die with faces marked 1, 2, 3, 4, 5 and 6 is rolled four times. Out of four face values obtained, the probability that the minimum face value is not less than 2 and the maximum face value is not greater than 5 is
How many cards must be selected from a standard deck of 52 cards to guarantee that at least three hearts are present among them?
Out of 8 gentlemen and 5 ladies, a committee of 5 is to be formed. Find the number of ways in which this can be done so as to include at least 3 ladies?
Two events A and B with probability 0.5 and 0.7 respectively, have joint probability of 0.4 the probability that neither A or B happens is
Three dices are thrown simultaneously. What is the probability that the sum of numbers is 15?
What is the probability of an event that is certain to occur?




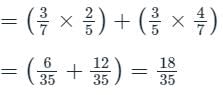
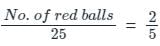
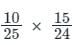 = 1/4
= 1/4