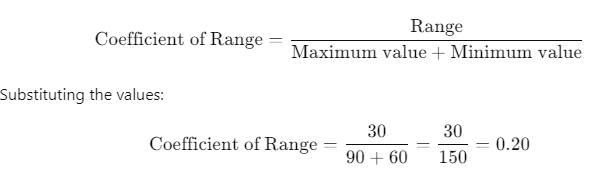Test: Measures Of Central Tendency And Dispersion- 1 - CDS MCQ
30 Questions MCQ Test - Test: Measures Of Central Tendency And Dispersion- 1
(Direction 1 - 21)Write down the correct answers. Each question carries one mark.
Q. Which of the following statements is correct?
When it comes to comparing two or more distributions we consider
Which one is difficult to compute?
Which one is an absolute measure of dispersion?
Which measure of dispersion is the quickest to compute?
Which measures of dispersions is not affected by the presence of extreme observations?
Which measure of dispersion is based on the absolute deviations only?
Which measure is based on only the central fifty percent of the observations?
Which measure of dispersion is based on all the observations?
The appropriate measure of dispersions for open – end classification is
The most commonly used measure of dispersion is
Which measure of dispersion has some desirable mathematical properties?
If the profits of a company remains the same for the last ten months, then the standard deviation of profits for these ten months would be ?
Which measure of dispersion is considered for finding a pooled measure of dispersion after combining several groups?
A shift of origin has no impact on
The range of 15, 12, 10, 9, 17, 20 is
The standard deviation of, 10, 16, 10, 16, 10, 10, 16, 16 is
For any two numbers SD is always
If all the observations are increased by 10, then
If all the observations are multiplied by 2, then
(Dirction 22 - 40) Write down the correct answers. Each question carries two marks.
Q. What is the coefficient of range for the following wages of 8 workers?
Rs.80, Rs.65, Rs.90, Rs.60, Rs.75, Rs.70, Rs.72, Rs.85.
If Rx and Ry denote ranges of x and y respectively where x and y are related by 3x+2y+10=0, what would be the relation between x and y?
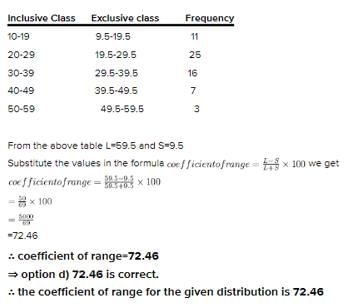
What is the coefficient of range for the following distribution?
If mean and mode of some data are 4 & 10 respectively, its median will be:
What is the value of mean deviation about mean for the following numbers?
5, 8, 6, 3, 4.
Median in set 6, 4, 2, 3, 4, 5, 5, 4 would be
The coefficient of mean deviation about mean for the first 9 natural numbers is
If the relation between x and y is 5y–3x = 10 and the mean deviation about mean for x is 12, then the mean deviation of y about mean is
If two variables x and y are related by 2x + 3y –7 =0 and the mean and mean deviation about mean of x are 1 and 0.3 respectively, then the coefficient of mean deviation of y about mean is