Test: Basic Concepts Of Differential And Integral Calculus- 2 - GRE MCQ
30 Questions MCQ Test - Test: Basic Concepts Of Differential And Integral Calculus- 2
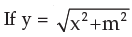 then y y1 (where y1 = dy/dx) is equal to
then y y1 (where y1 = dy/dx) is equal to
The derivative of (x2–1)/x is
The differential coefficients of (x2 +1)/x is
If y = 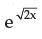 then
then 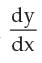 is equal to _____.
is equal to _____.
If x = (1 – t2 )/(1 + t2) y = 2t/(1 + t2) then dy/dx at t =1 is _____________.
f(x) = x2/ex then f ’(1) is equal to _____________.
Evaluate ∫ 5x2 dx and the answer will be
Integration of 3 – 2x – x4 will become
Given f(x) = 4x3 + 3x2 – 2x + 5, ∫ f(x) dx is
Evaluate ∫ (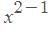 ) dx . The value is
) dx . The value is
∫ (1 - 3x) (1 + x) dx is equal to
The integral of px3 + qx2 + rk + w/x is equal to
Use method of substitution to integrate the function f(x) = (4x + 5)6 and the answer is
Use method of substitution to evaluate ∫ x (x2 + 4)5dx and the answer is
Integrate (x + a)n and the result will be
∫ 8x2/ (x3 + 2)3 dx is equal to
Using method of partial fraction find the integration of f(x) when f(x) = 1/x2 – a2 and the answer is
Use integration by parts to evaluate ∫ x2 e3x dx and the answer is
∫ logx dx is equal to
∫ (logx)2 dx and the result is
Using method of partial fraction to evaluate ∫ (x + 5) dx/(x + 1) (x + 2)2 and the final answer becomes



















