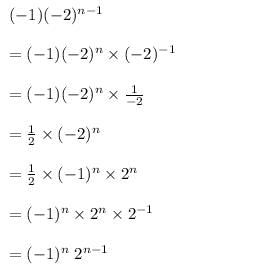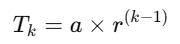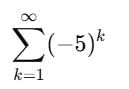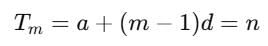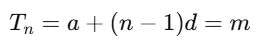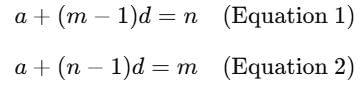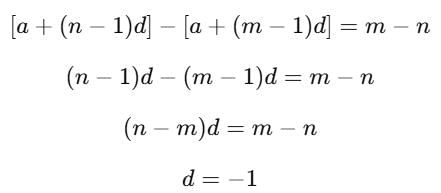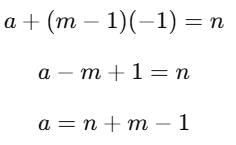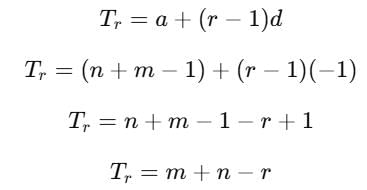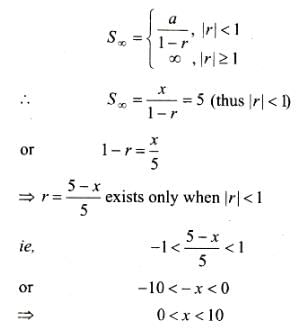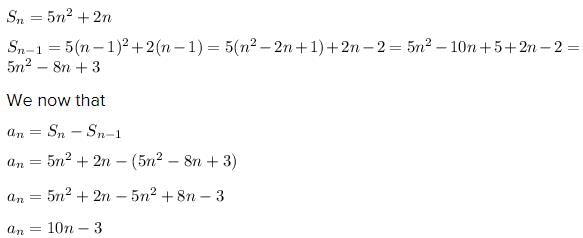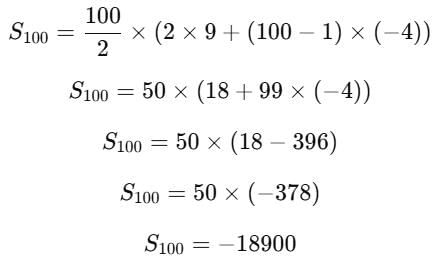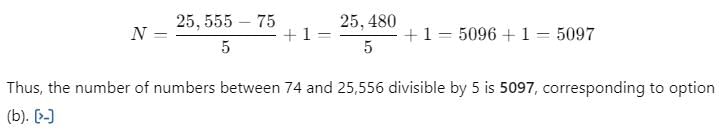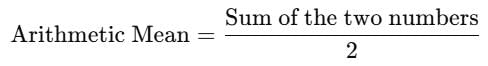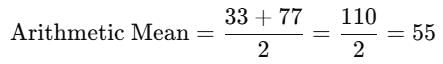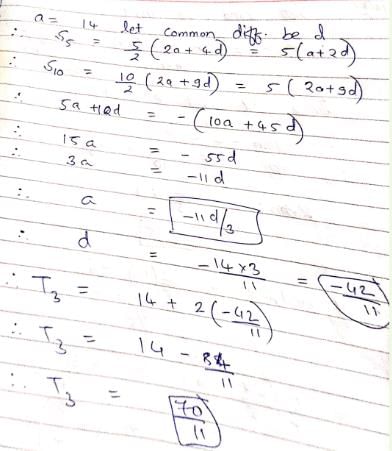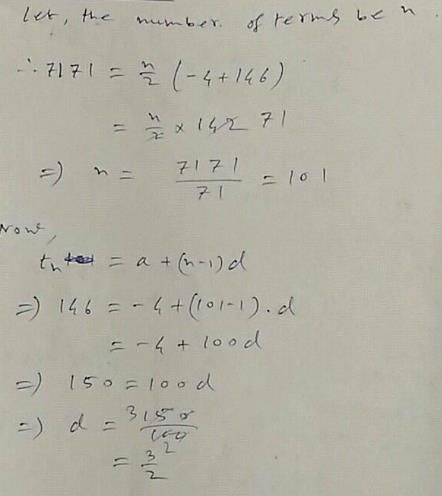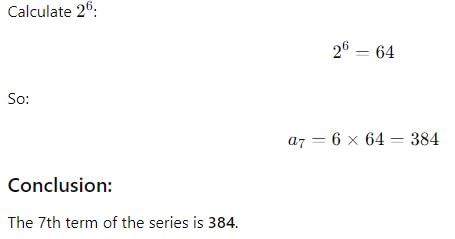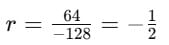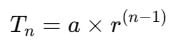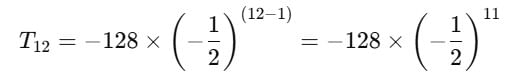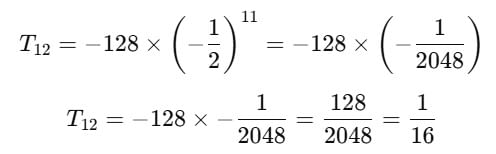Test: Arithmetic And Geometric Progressions - 1 - CA Foundation MCQ
30 Questions MCQ Test - Test: Arithmetic And Geometric Progressions - 1
Choose the most appropriate option ( a ), ( b ) , ( c ) or (d)
The nth element of the sequence 1, 3, 5, 7,….…..Is
The nth element of the sequence –1, 2, –4, 8 ….. is
The arithmetic mean between a and 10 is 30, the value of ‘a’ should be
–5, 25, –125 , 625, ….. can be written as
The first three terms of sequence when nth term tn is n2 – 2n are
Which term of the progression –1, –3, –5, …. Is –39
The value of x such that 8x + 4, 6x – 2, 2x + 7 will form an AP is
The mth term of an A. P. is n and nth term is m. The r th term of it is
An infinite GP has first term x and sum 5, then x belongs to
The nth term of the series whose sum to n terms is 5n2 + 2n is
The 20th term of the progression 1, 4, 7, 10.................is
The last term of the series 5, 7, 9,….. to 21 terms is
The last term of the A.P. 0.6, 1.2, 1.8,… to 13 terms is
The sum of the series 9, 5, 1,…. to 100 terms is
The two arithmetic means between –6 and 14 is
The sum of three integers in AP is 15 and their product is 80. The integers are
The sum of n terms of an AP is 3n2 + 5n. A.P. is
The number of numbers between 74 and 25556 divisible by 5 is
The pth term of an AP is (3p – 1)/6. The sum of the first n terms of the AP is
The arithmetic mean between 33 and 77 is
The 4 arithmetic means between –2 and 23 are
The first term of an A.P is 14 and the sums of the first five terms and the first ten terms are equal is magnitude but opposite in sign. The 3rd term of the AP is
The sum of a certain number of terms of an AP series 8, 6, 4, …… is -52. The number of terms is
The 1st and the last term of an AP are –4 and 146. The sum of the terms is 7171. The number of terms is
The sum of the series 3 ½ + 7 + 10 ½ + 14 + …. To 17 terms is
The 7th term of the series 6, 12, 24,……is
t12 of the series –128, 64, –32, ….is
The 4th term of the series 0.04, 0.2, 1, … is
The last term of the series 1, 2, 4,…. to 10 terms is