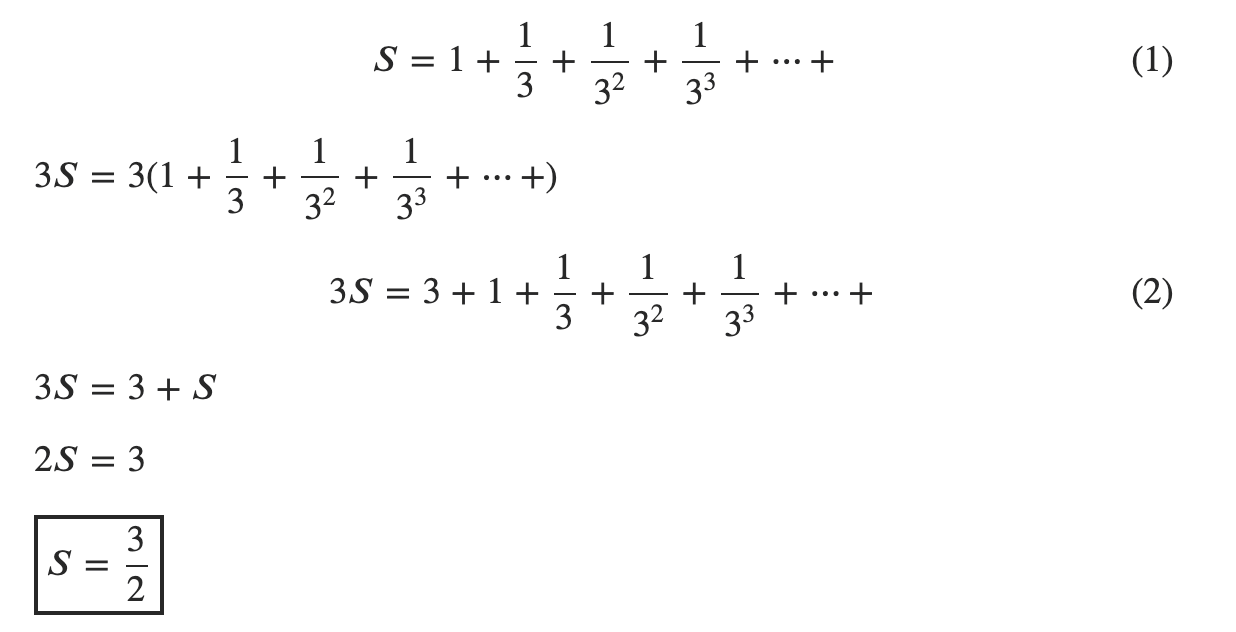Test: Arithmetic And Geometric Progressions - 2 - CA Foundation MCQ
30 Questions MCQ Test - Test: Arithmetic And Geometric Progressions - 2
Sum of n terms of the series 0.1 + 0.11 + 0.111 + … is
The sum of the first 20 terms of a G. P is 244 times the sum of its first 10 terms. The common ratio is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Sum of the series 1 + 3 + 9 + 27 +….is 364. The number of terms is
The product of 3 numbers in G P is 729 and the sum of squares is 819. The numbers are
The sum of the series 1 + 2 + 4 + 8 + .. to n term
The sum of the infinite GP 14 – 2 + 2/7 – 2/49 + … is
The sum of the infinite G. P. 1 - 1/3 + 1/9 - 1/27 +... is
The number of terms to be taken so that 1 + 2 + 4 + 8 + will be 8191 is
Four geometric means between 4 and 972 are
Three numbers are in AP and their sum is 21. If 1, 5, 15 are added to them respectively, they form a G. P. The numbers are
The sum of 1 + 1/3 + 1/32 + 1/33 + … + 1/3 n –1 is
The sum of the infinite series 1 + 2/3 + 4/9 + .. is
The sum of the first two terms of a G.P. is 5/3 and the sum to infinity of the series is 3. The common ratio is
If p, q and r are in A.P. and x, y, z are in G.P. then xq–r. y r–p. zp–q is equal to
The sum of three numbers in G.P. is 70. If the two extremes by multiplied each by 4 and the mean by 5, the products are in AP. The numbers are
The sum of 3 numbers in A.P. is 15. If 1, 4 and 19 be added to them respectively, the results are is G. P. The numbers are
Given x, y, z are in G.P. and xp = yq = zσ, then 1/p , 1/q, 1/σ are in
If the terms 2x, (x+10) and (3x+2) be in A.P., the value of x is
If A be the A.M. of two positive unequal quantities x and y and G be their G. M, then
The A.M. of two positive numbers is 40 and their G. M. is 24. The numbers are
Three numbers are in A.P. and their sum is 15. If 8, 6, 4 be added to them respectively, the numbers are in G.P. The numbers are
The sum of four numbers in G. P. is 60 and the A.M. of the 1st and the last is 18. The numbers are
A sum of Rs. 6240 is paid off in 30 instalments such that each instalment is Rs. 10 more than the proceeding installment. The value of the 1st instalment is
The sum of 1.03 + (1.03)2 + (1.03)3 + …. to n terms is
If x, y, z are in A.P. and x, y, (z + 1) are in G.P. then
The numbers x, 8, y are in G.P. and the numbers x, y, –8 are in A.P. The value of x and y are
The nth term of the series 16, 8, 4,…. Is 1/217. The value of n is
The sum of n terms of a G.P. whose first terms 1 and the common ratio is 1/2 , is equal to 
t4 of a G.P. in x, t10 = y and t16 = z. Then
Top Courses for CA Foundation
Important Questions for Arithmetic And Geometric Progressions - 2
Arithmetic And Geometric Progressions - 2 MCQs with Answers
Online Tests for Arithmetic And Geometric Progressions - 2
|
© EduRev
|
Education Revolution
|
|
