Test: Regular Expressions & Finite Automata- 2 - Computer Science Engineering (CSE) MCQ
20 Questions MCQ Test - Test: Regular Expressions & Finite Automata- 2
Which one of the following is TRUE?
Which of the regular expressions given below represent the following DFA?
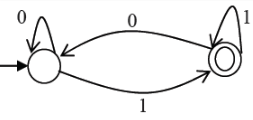
I) 0*1(1+00*1)*
II) 0*1*1+11*0*1
III) (0+1)*1
II) 0*1*1+11*0*1
III) (0+1)*1
Q. Which one of the following is CORRECT?
Let L1 = {w ∈ {0,1}∗ | w has at least as many occurrences of (110)’s as (011)’s}.
Let L2 = { ∈ {0,1}∗ | w has at least as many occurrences of (000)’s as (111)’s}.
Q. Which one of the following is TRUE?
The length of the shortest string NOT in the language (over Σ = {a, b}) of the following regular expression is ______________.
a*b*(ba)*a*
If s is a string over (0 + 1)* then let n0(s) denote the number of 0’s in s and n1(s) the number of 1’s in s. Which one of the following languages is not regular?
Consider the regular language L = (111 + 11111)*. The minimum number of states in any DFA accepting this languages is:
Consider the machine M:
Q. The language recognized by M is :
Let Nf and Np denote the classes of languages accepted by non-deterministic finite automata and non-deterministic push-down automata, respectively. Let Df and Dp denote the classes of languages accepted by deterministic finite automata and deterministic push-down automata, respectively. Which one of the following is TRUE?
The following diagram represents a finite state machine which takes as input a binary number from the least significant bit.
Q. Which one of the following is TRUE?
The following finite state machine accepts all those binary strings in which the number of 1's and 0's are respectively.
The regular expression 0*(10*)* denotes the same set as
Consider the following deterministic finite state automaton M.
Let S denote the set of seven bit binary strings in which the first, the fourth, and the last bits are 1. The number of strings in S that are accepted by M is
Consider the NFA M shown below.
Q. Let the language accepted by M be L. Let L1 be the language accepted by the NFA M1, obtained by changing the accepting state of M to a non-accepting state and by changing the non-accepting state of M to accepting states. Which of the following statements is true ?
The Finite state machine described by the following state diagram with A as starting state, where an arc label is x / y and x stands for 1-bit input and y stands for 2- bit output
The smallest finite automation which accepts the language {x | length of x is divisible by 3} has :
Consider the following two statements:
Given an arbitary non-deterministic finite automaton (NFA) with N states, the maximum number of states in an equivalent minimized DFA is at least
Consider a DFA over ∑ = {a, b} accepting all strings which have number of a’s divisible by 6 and number of b’s divisible by 8. What is the minimum number of states that the DFA will have?














