Test: Asymptotic Worst Case Time & Space Complexity- 2 - Computer Science Engineering (CSE) MCQ
20 Questions MCQ Test - Test: Asymptotic Worst Case Time & Space Complexity- 2
A list of n string, each of length n, is sorted into lexicographic order using the merge-sort algorithm. The worst case running time of this computation is
In quick sort, for sorting n elements, the (n/4)th smallest element is selected as pivot using an O(n) time algorithm.
Q.
What is the worst case time complexity of the quick sort?
Q.
What is the worst case time complexity of the quick sort?
Consider the Quicksort algorithm. Suppose there is a procedure for finding a pivot element which splits the list into two sub-lists each of which contains at least one-fifth of the elements. Let T(n) be the number of comparisons required to sort n elements. Then
Consider the following functions:
f(n) = 2^n
g(n) = n!
h(n) = n^logn
Q. Which of the following statements about the asymptotic behavior of f(n), g(n), and h(n) is true?
In the following C function, let n >= m.
Q. How many recursive calls are made by this function?
Which of the following sorting algorithms has the lowest worst-case complexity?
Consider the following functions
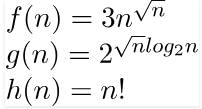
Consider the following three claims I (n + k)^m = θ(n^m), where k and m are constants II 2^(n + 1) = 0(2^n) III 2^(2n + 1) = 0(2^n) Which of these claims are correct?
Let s be a sorted array of n integers. Let t(n) denote the time taken for the most efficient algorithm to determined if there are two elements with sum less than 1000 in s. which of the following statements is true?
Consider the following function
Q. What is the returned value of the above function?
The number of elements that can be sorted in time using heap sort is
Consider the following two functions. What are time complexities of the functions?
In quick sort, for sorting n elements, the (n/4)th smallest element is selected as pivot using an O(n) time algorithm. What is the worst case time complexity of the quick sort?
Consider the Quicksort algorithm. Suppose there is a procedure for finding a pivot element which splits the list into two sub-lists each of which contains at least one-fifth of the elements. Let T(n) be the number of comparisons required to sort n elements. Then
Consider the following segment of C-code:
Q. The number of comparisons made in the execution of the loop for any n > 0 is: Base of Log is 2 in all options.
Consider the following C-program fragment in which i, j and n are integer variables.
for (i = n, j = 0; i >0; i /= 2, j += i);
Q. Let val(j) denote the value stored in the variable j after termination of the for loop. Which one of the following is true?
The minimum number of comparisons required to find the minimum and the maximum of 100 numbers is _________________.
Consider the following pseudo code. What is the total number of multiplications to be performed?
You have an array of n elements. Suppose you implement quicksort by always choosing the central element of the array as the pivot. Then the tightest upper bound for the worst case performance is
Consider the following C-function:
Q. The space complexity of the above function is:



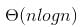
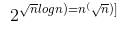 f(n) and g(n) are of same asymptotic order and following statements are true. f(n) = O(g(n)) g(n) = O(f(n)). (a) and (b) are false because n! is of asymptotically higher order than
f(n) and g(n) are of same asymptotic order and following statements are true. f(n) = O(g(n)) g(n) = O(f(n)). (a) and (b) are false because n! is of asymptotically higher order than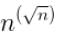 .
.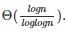 , the value of θ(m * Logm) will be
, the value of θ(m * Logm) will be 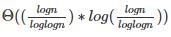 which will be [
which will be [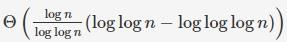 which is θ(Log n)
which is θ(Log n)










