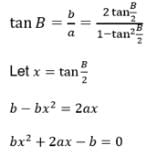Test: Trigonometric Functions - JEE MCQ
25 Questions MCQ Test - Test: Trigonometric Functions
If in a triangle ABC, (s − a) (s − b) = s (s − c), then angle C is equal to
The angles of a triangle are as 1 : 2 : 7, then ratio of greatest side to least side is
If the sides of a triangle are 13, 7, 8 the greatest angle of the triangle is
There exists a triangle ABC satisfying the conditions:
In a ΔABC, (b +c) cos A + (c + a) cos B + (a + b) cos C is equal to
The perimeter of a triangle ABC is 6 times the arithmetic mean of the sines of its angles. If the side b is 2, then the angle B is
The area of a triangle is 80cm2 and its perimeter is 8 cm. The radius of its inscribed circle is
If the angles of a triangle be in the ratio 1 : 4 : 5, then the ratio of the greatest side to the smallest side is
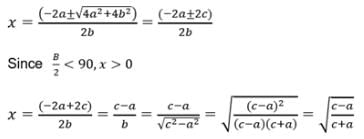
If a = 4, b = 3 and A = 60∘, then c is a root of the equation
If the sides of a triangle be 2x + 1, x2- 1 and x2 + x + 1, then the greatest angle is
If in a triangle ABC, acos2 (c/2) + ccos2 (A/2) = 3b/2, then its sides a, b, c are in
In a ΔABC, if a sin A = b sin B then the triangle is
If in a ΔABC, a cos A = b cos B, then the triangle is
In a triangle ABC, a = 2b and ∠A = 3∠ B then angle A is
In a triangle ABC, AD is the median A to BC, then its length is equal to
If cos A + cos B = , then the sides of the triangle ABC are in
ABC is an equilateral triangle of each side a (> 0). The inradius of the triangle is
In any ΔABC, the expression (a + b + c) (a + b – c) (b + c – a) (c + a – b) is equal to


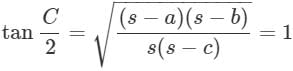
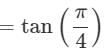
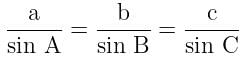
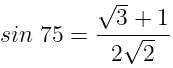
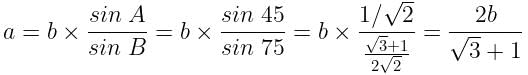
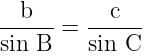
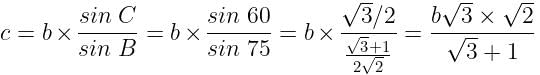
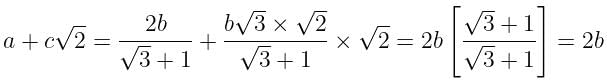


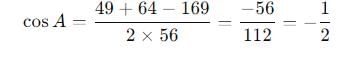
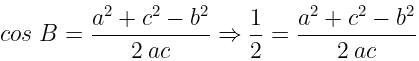
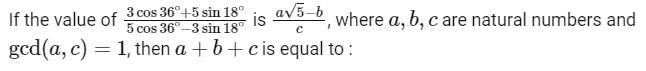



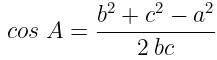
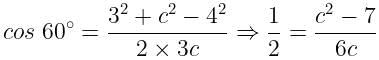
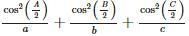 is equal to
is equal to