Test: System of Particles and Rotational Motion (September 10) - NEET MCQ
15 Questions MCQ Test - Test: System of Particles and Rotational Motion (September 10)
A constant torque of 1000 N-m turns a wheel of the moment of inertia 200 kg-m2 about an axis through its centre. Its angular velocity after 3 seconds is:
[2001]
[2001]
If the linear density (mass per unit length) of a rod of length 3m is proportional to x, where x is the distance from one end of the rod, the distance of the centre of gravity of the rod from this end is:
[2002]
[2002]
A composite disc is to be made using equal masses of aluminium and iron so that it has as high a moment of inertia as possible. This is possible when:
[2002]
[2002]
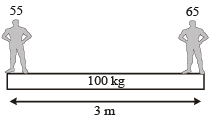
Two persons of masses 55 kg and 65 kg respectively, are at the opposite ends of a boat. The length of the boat is 3.0 m and weighs 100 kg. The 55 kg man walks up to the 65 kg man and sits with him. If the boat is in still water the centre of mass of the system shifts by:
[2012]
A circular platform is mounted on a frictionless vertical axle. Its radius R = 2 m and its moment of inertia about the axle is 200 kgm2. It is initially at rest. A 50 kg man stands on the edge of the platform and begins to walk along the edge at the speed of 1 ms–1 relative to the ground. Time taken by the man to complete one revolution is:
The moment of inertia of a uniform circular disc is maximum about an axis perpendicular to the disc and passing through:
[2012M]
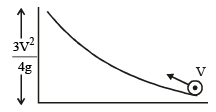
A small object of uniform density rolls up a curved surface with an initial velocity ‘ν’. It reaches up to a maximum height of 3v2 / 4g with respect to the initial position. The object is a:
[2013]
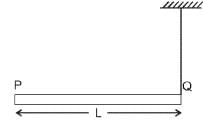
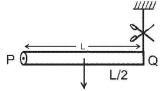
A rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in the figure. When the string is cut, the initial angular acceleration of the rod is:
[2013]
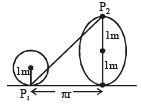
Two discs are rotating about their axes, normal to the discs and passing through the centres of the discs. Disc D1 has 2 kg mass and 0.2 m radius and initial angular velocity of 50 rad s–1. Disc D2 has 4kg mass, 0.1 m radius and initial angular velocity of 200 rad s–1. The two discs are brought in contact face to face, with their axes of rotation coincident. The final angular velocity (in rad s–1) of the system is:
[2013]
The ratio of radii of gyration of a circular ring and a circular disc, of the same mass and radius, about an axis passing through their centres and perpendicular to their planes are:
[2013]
A wheel of radius 1m rolls for war d half a revolution on horizontal ground. The magnitude of the displacement of the point of the wheel initially in contact with the ground is:
[2002]
A disc is rotating with angular velocity ω. If a child sits on it, what is conserved?
[2002]
When a mass is rotating in a plane about a fixed point, its angular momentum is directed along:
[2012]
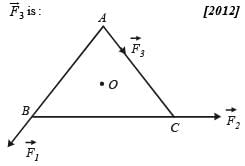
ABC is an equilateral triangle with O as its centre. represent three forces acting along the sides AB, BC and AC respectively. If the total torque about O is zero the magnitude of
represent three forces acting along the sides AB, BC and AC respectively. If the total torque about O is zero the magnitude of
Three masses are placed on the x-axis: 300g at origin, 500g at x = 40cm and 400g at x = 70 cm.The distance of the centre of mass from the origin is:
[2012M]


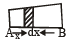
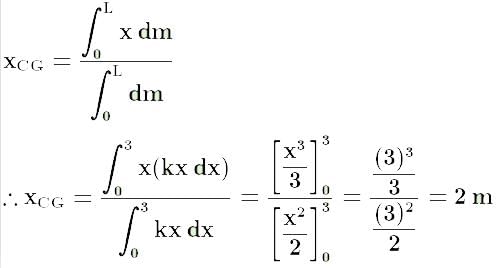

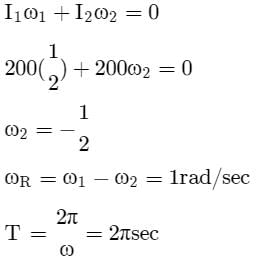
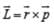
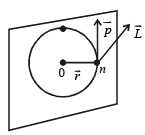
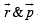 .
.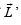 will be perpendicular to this plane.
will be perpendicular to this plane.















