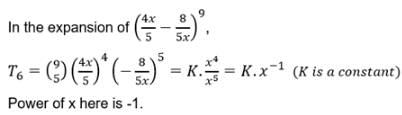Test: Binomial Theorem- 2 - JEE MCQ
25 Questions MCQ Test - Test: Binomial Theorem- 2
The coefficient of second, third and fourth terms in the binomial expansion of (1+x)n(‘n’, a + ve integer) are in A.P.., if n is equal to
The coefficient of x17 in the expansion of (x- 1) (x- 2) …..(x – 18) is
If the coefficients of (r +1)th term and (r + 3)th term in the expansion of (1+x)2n be equal then
In the expansion of (1+x)60, the sum of coefficients of odd powers of x is
Let n ∈ Q an n ∉ N,n ≠ 0, a > 0, then the expansion of (a+x)n in powers of x is valid if
The coefficient of x99 in (x+1)(x+3)(x+5)………..(x+199) is
If the expansion of in powers of x contains the term x2r, then n−2r is
If rth ,(r+1)th and (r+2)th terms in the expansion of (1+x)n are in A.P. then
Coefficient of a2b5 in the expansion of (a+b)3(a−2b)4 is
In the expansion of(1+x)11, the 5th term is 24 times the 3rd term . The value of x is
The sum of coefficients in the expansion of (x+2y+z)n is (n being a positive integer)
If the rth term in the expansion of contains x4 then r is equal to
The coefficients of xn in the expansion of (1+2x + 3x2 + ........)1/2 is
The index of the power of x that occurs in the 7th term from the end in the expansion of
The index of the power of x that occurs in the 6th term in the expansion of
If in the expansion of(1+x)43, the coefficients of (2r+1)th and (r+2)th terms are equal, then r is equal to


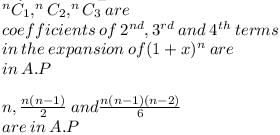
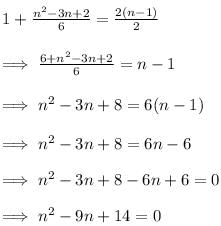

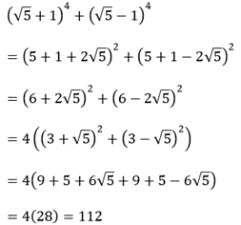
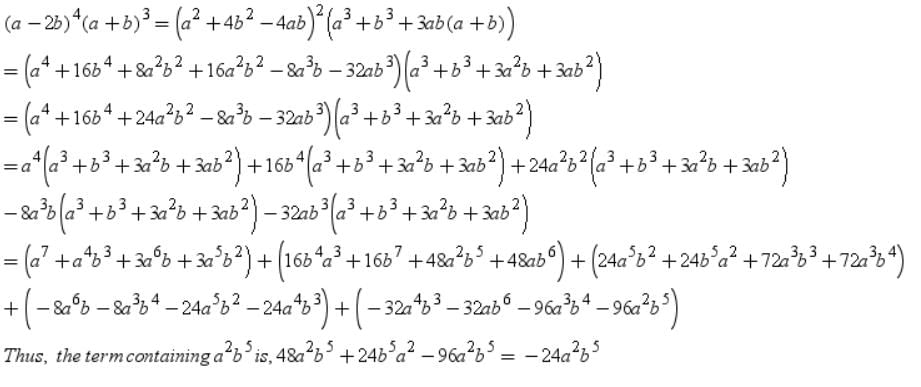
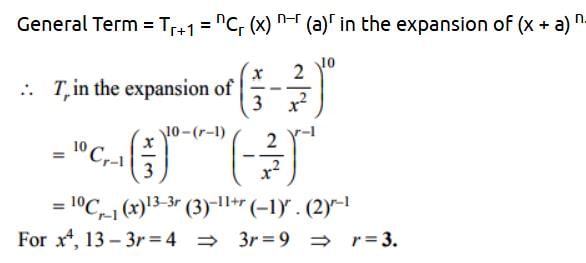
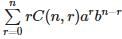 is equal to
is equal to 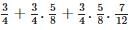 + ........, then z2 + 2z is equal to
+ ........, then z2 + 2z is equal to